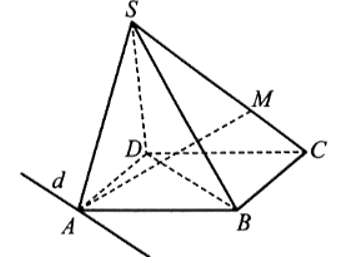
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm chuyển động trên cạnh SC (M khác C)
Bài 26 trang 104 SBT Toán 11: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm chuyển động trên cạnh SC (M khác C), (P) là mặt phẳng chứa đường thẳng AM và song song với BD. Chứng minh rằng mặt phẳng (P) luôn đi qua một đường thẳng cố định khi điểm M chuyển động trên cạnh SC.