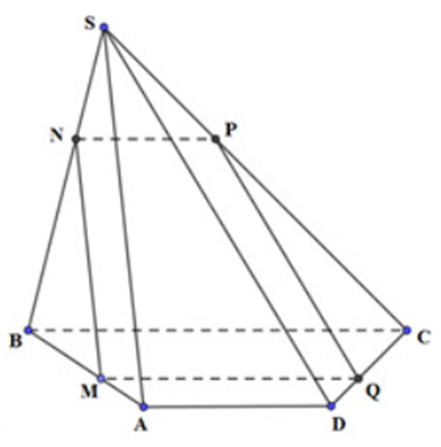
+) Dựng thiết diện:

Qua M kẻ MQ song song BC (Q ∈ DC), kẻ MN song song SA (N ∈ SB)

Qua N kẻ NP song song BC (P ∈ SC)

Khi đó, (MNPQ) là mặt phẳng qua M và song song BC, SA

⇒ (MNPQ) ≡ (α)

Thiết diện của hình chóp bị cắt bởi mặt phẳng (α) là tứ giác MNPQ.

+) Tính diện tích thiết diện:

Ta có: NP // MQ (cùng song song BC) ⇒ MNPQ là hình thang

ΔSAD đều ⇒ SA = SD = AD = a

ABCD là hình thang, MQ // BC ⇒ \(\frac{{CQ}}{{DC}} = \frac{{BM}}{{AB}} = \frac{{BN}}{{SB}} = \frac{2}{3}\)

MN // SA ⇒ \(\frac{{MN}}{{SA}} = \frac{{BM}}{{AB}} = \frac{2}{3}\) ⇒ \(MN = \frac{2}{3}SA = \frac{2}{3}a\)

NP // BC ⇒ \(\frac{{NP}}{{BC}} = \frac{1}{3}\) ⇒ \(NP = \frac{1}{3}BC = \frac{2}{3}a\) và \(\frac{{PC}}{{SC}} = \frac{{NB}}{{SB}} = \frac{2}{3}\) ⇒ \(\frac{{PC}}{{SC}} = \frac{{CQ}}{{DC}} = \frac{2}{3}\)

⇒ \(\frac{{PQ}}{{SD}} = \frac{2}{3}\) ⇒ \(PQ = \frac{2}{3}SD = \frac{2}{3}a.\)

Gọi I, J lần lượt là trung điểm của BM và CQ.

Giả sử MQ có độ dài bằng x. Khi đó, do IJ là đường trung bình của hình thang BCQM

⇒ \(IJ = \frac{{MQ + BC}}{2} = \frac{{x + 2a}}{2}\)

Do MQ là đường trung bình của hình thang IJDA ⇒ 2MQ = IJ + AD

⇔ \(2x = \frac{{x + 2a}}{2} + a\) ⇔ 4x = x + 2a + 2a ⇔ \(x = \frac{4}{3}a\)

⇒ \(MQ = \frac{4}{3}a\)

Xét hình thang MNPQ có: NP = MN = PQ = \(\frac{2}{3}a,\) \(MQ = \frac{4}{3}a\) ⇒ MNPQ là hình thang cân.

Kẻ MH, NK vuông góc với PQ (H, K ∈ PQ)

⇒ \(QH = PK = \frac{{PQ - MN}}{2} = \frac{{\frac{4}{3}a - \frac{2}{3}a}}{2} = \frac{a}{3}\)

⇒ \(MH = \sqrt {M{Q^2} - Q{H^2}} = \sqrt {{{\left( {\frac{2}{3}a} \right)}^2} - {{\left( {\frac{1}{3}a} \right)}^2}} = \sqrt {\frac{{{a^2}}}{3}} = \frac{{a\sqrt 3 }}{3}.\)

Diện tích hình thang MNPQ: \(S = \frac{1}{2}\left( {MN + PQ} \right).MH = \frac{1}{2}.\left( {\frac{2}{3}a + \frac{4}{3}a} \right).\frac{{a\sqrt 3 }}{3} = \frac{{{a^2}\sqrt 3 }}{3}.\)