Cho hình chóp S.ABC, đáy ABC đều cạnh 2a. Cạnh bên SA vuông góc với mặt đáy. Góc giữa SB và (ABC) là 60°. Tính thể tích S.ABC.

Trả lời

Lời giải

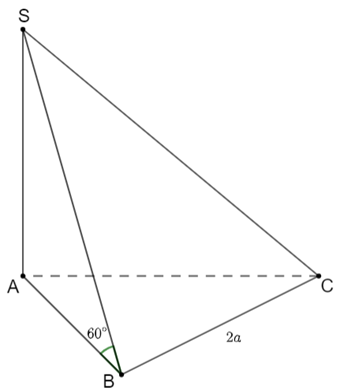
Ta có SA ^ (ABC)

Suy ra \[\left( {\widehat {SA;\;\left( {ABC} \right)}} \right) = \widehat {SBA} = 60^\circ \]

\( \Rightarrow \frac{{SA}}{{AB}} = \tan \widehat {SBA} = \tan 60^\circ = \sqrt 3 \)

\( \Rightarrow SA = AB\sqrt 3 = 2a\sqrt 3 \)

Diện tích đáy ABC là tam giác đều cạnh 2a là:

\({S_{ABC}} = \frac{{{{\left( {2a} \right)}^2}\sqrt 3 }}{4} = {a^2}\sqrt 3 \)

Thể tích hình chóp S.ABC là: \({V_{S.ABC}} = \frac{1}{3}SA.\,{S_{ABC}} = \frac{1}{3}\,.\,2a\sqrt 3 \,.\,{a^2}\sqrt 3 = 2{a^3}\).