Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BA = 3a, BC = 4a. Mặt phẳng (SBC) vuông góc với (ABC). Biết SB = \(2a\sqrt 3 \) và \(\widehat {SBC} = 30^\circ \). Tính khoảng cách từ B đến (SAC) theo a.
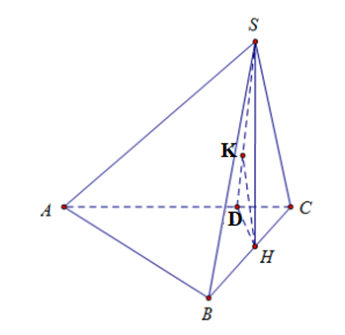
Hạ HD ⊥ AC (D thuộc AC) và HK ⊥ SD (K thuộc SD), ta có:
HK ⊥ (SAC) suy ra: d(H;(SAC)) = HK
Trong tam giác SHD, ta có: \(\frac{1}{{H{K^2}}} = \frac{1}{{H{D^2}}} + \frac{1}{{S{H^2}}}\)
Suy ra: HK = \(\frac{{SH.HD}}{{\sqrt {S{H^2} + H{D^2}} }}\)
Hai tam giác ABC và HDC đồng dạng nên: \(\frac{{HD}}{{AB}} = \frac{{HC}}{{AC}}\)
⇔ HD = \(\frac{{AB\left( {BC - BH} \right)}}{{\sqrt {A{B^2} + B{C^2}} }} = \frac{{3a\left( {4a - 3a} \right)}}{{\sqrt {9{a^2} + 16{a^2}} }} = \frac{{3a}}{5}\)
HK = \[\frac{{a\sqrt 3 .\frac{{3a}}{5}}}{{\sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {{\left( {\frac{{3a}}{5}} \right)}^2}} }} = \frac{{3a\sqrt 7 }}{{14}}\]
\(\frac{{d\left( {B,\left( {SAC} \right)} \right)}}{{d\left( {H,\left( {SAC} \right)} \right)}} = \frac{{BC}}{{HC}} = \frac{{4a}}{a} = 4\)
d(B,(SAC)) = 4d(H,(SAC)) = \[4.\frac{{3a\sqrt 7 }}{{14}} = \frac{{6a\sqrt 7 }}{7}\].