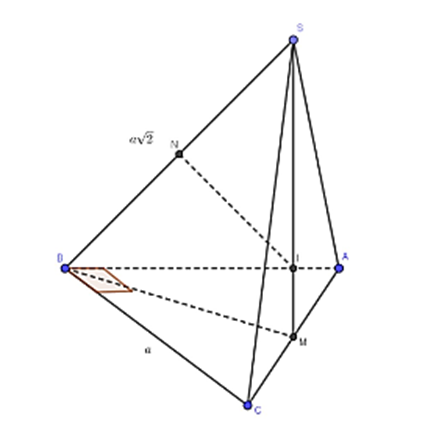
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a. Cạnh bên SA = \[a\sqrt 2 \], hình chiếu của điểm S lên mặt phẳng đáy trùng với trung điểm của cạnh huyền AC. Bán kính mặt cầu ngoại tiếp khối chóp S.ABC.
ΔABC vuông cân tại B có AB = a
\[ \Rightarrow AC = a\sqrt 2 \]
Gọi M là trung điểm AC
\[ \Rightarrow MA = MB = MC = \frac{1}{2}AC = a\sqrt 2 ;\,\,SM \bot (ABC)\]
Þ SM là trục của mặt phẳng đáy (ABC)
Gọi N là trung điểm SA
Trong mp(SAM) kẻ NI ⊥ SA (I ∈ SM)
Þ I là tâm mặt cầu ngoại tiếp khối chóp S.ABC
Ta có: ΔSNI ᔕ ΔSMA (g.g)
\[ \Rightarrow \frac{{SN}}{{SM}} = \frac{{SI}}{{SA}}\]
\[ \Rightarrow SI = R = \frac{{SA.SN}}{{SM}}\]
\[ \Rightarrow R = \frac{{S{A^2}}}{{2SM}} = \frac{{S{A^2}}}{{2\sqrt {S{A^2} - A{M^2}} }}\]
\[ \Rightarrow R = \frac{{a\sqrt 6 }}{3}\]
Vậy \[R = \frac{{a\sqrt 6 }}{3}\].