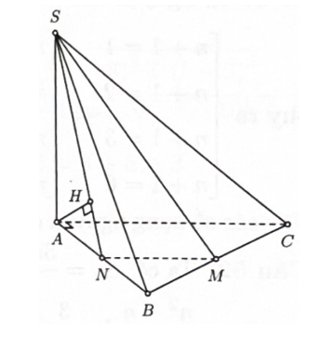
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB vuông góc với mặt phẳng đáy

8 17/11/2024

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB vuông góc với mặt phẳng đáy và $S A = \sqrt{3} a .$ Gọi M là trung điểm BC. Khoảng cách giữa hai đường thẳng AC và SM bằng

\frac{\sqrt{39} a}{12} .

\frac{\sqrt{2} a}{3} .

\frac{\sqrt{39} a}{13} .

\frac{\sqrt{2} a}{2} .

Trả lời

Gọi N là trung diểm AB. Kẻ $A H ⊥ S N .$

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB vuông góc với mặt phẳng đáy (ảnh 1)

Vì $M N / / A C, M N \subset (S M N)$ nên $A C / / (S M N)$

$\Rightarrow d (S M; A C) = d (A C; (S M N)) = d (A; (S M N))$

Ta có $\{\begin{array}{l} M N ⊥ A B \\ M N ⊥ S A \end{array} \Rightarrow M N ⊥ (S A B) \Rightarrow M N ⊥ A H .$

Từ đó suy ra $A H ⊥ (S M N) \Rightarrow d (S M; A C) = A H .$

Lại có $\frac{1}{A H^{2}} = \frac{1}{A S^{2}} + \frac{1}{A N^{2}} = \frac{13}{3 a^{2}} \Rightarrow A H = \frac{\sqrt{39} a}{13} .$

Chọn C

Đề thi Đánh giá tư duy tốc chiến Đại học Bách khoa năm 2023-2024 có đáp án (Đề 8)

Câu hỏi cùng chủ đề

Ông Bộ làm lan can ban công ngôi nhà của mình bằng một tấm kính cường lực. Tấm kính đó là một phần của mặt xung quanh của một hình

Đề thi Đánh giá tư duy tốc chiến Đại học Bách khoa năm 2023-2024 có đáp án (Đề 8)

6 5 ngày trước

Trong không gian Oxyz, cho tam giác ABC nội tiếp đường tròn tâm I(2;3; −4), trực tâm H(3; 0; 1). Biết A(1; −2;0), phương trình đường thẳng BC là

Đề thi Đánh giá tư duy tốc chiến Đại học Bách khoa năm 2023-2024 có đáp án (Đề 8)

5 5 ngày trước

Trong không gian Oxyz, cho các điểm A(1; 3;-2), B(0; 4; 7), C(5;-1; 2) và mặt phẳng (P): x + y + z – 2 = 0.

Đề thi Đánh giá tư duy tốc chiến Đại học Bách khoa năm 2023-2024 có đáp án (Đề 8)

5 5 ngày trước

Trong không gian Oxyz, cho ba điểm A(1; 1; 1), B(−1; 2; 0), C(2; –3; 2). Tập hợp tất cả các điểm M cách đều ba điểm A, B, C là một đường thẳng

Đề thi Đánh giá tư duy tốc chiến Đại học Bách khoa năm 2023-2024 có đáp án (Đề 8)

5 5 ngày trước

Có bao nhiêu số phức z= x+yi ( x , y thuộc Z) thỏa mãn: | z- 1-i | lớn hơn bằng 2 và | z^2 -z + 1- i | bé hơn bằng 4 ?

Đề thi Đánh giá tư duy tốc chiến Đại học Bách khoa năm 2023-2024 có đáp án (Đề 8)

5 5 ngày trước

Cho số phức z= a+ bi , z khác 0 thỏa mãn1-i / z là số thực và | z- 3i | - | z-3-2i| =2

Đề thi Đánh giá tư duy tốc chiến Đại học Bách khoa năm 2023-2024 có đáp án (Đề 8)

7 5 ngày trước

Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc v1(t) = 2t (m/s). Đi được 12 giây, người lái xe phát hiện chướng ngại

Đề thi Đánh giá tư duy tốc chiến Đại học Bách khoa năm 2023-2024 có đáp án (Đề 8)

4 5 ngày trước

Hình elip được ứng dụng nhiều trong thực tiễn, đặc biệt là kiến trúc xây dựng như đấu trường La Mã, tòa nhà Ellipse Tower Hà Nội

Đề thi Đánh giá tư duy tốc chiến Đại học Bách khoa năm 2023-2024 có đáp án (Đề 8)

6 5 ngày trước

Cho cấp số nhân (un) có số hạng đầu là u1 và công bội là q là số dương thỏa mãn

Đề thi Đánh giá tư duy tốc chiến Đại học Bách khoa năm 2023-2024 có đáp án (Đề 8)

6 5 ngày trước

Tổng n số hạng đầu tiên của một cấp số cộng là Sn = 3n^2 -19n /4 với n thuộc N*

Đề thi Đánh giá tư duy tốc chiến Đại học Bách khoa năm 2023-2024 có đáp án (Đề 8)

4 5 ngày trước

Xem tất cả

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB vuông góc với mặt phẳng đáy

Trả lời

Câu hỏi cùng chủ đề

Ông Bộ làm lan can ban công ngôi nhà của mình bằng một tấm kính cường lực. Tấm kính đó là một phần của mặt xung quanh của một hình

Trong không gian Oxyz, cho tam giác ABC nội tiếp đường tròn tâm I(2;3; −4), trực tâm H(3; 0; 1). Biết A(1; −2;0), phương trình đường thẳng BC là

Trong không gian Oxyz, cho các điểm A(1; 3;-2), B(0; 4; 7), C(5;-1; 2) và mặt phẳng (P): x + y + z – 2 = 0.

Trong không gian Oxyz, cho ba điểm A(1; 1; 1), B(−1; 2; 0), C(2; –3; 2). Tập hợp tất cả các điểm M cách đều ba điểm A, B, C là một đường thẳng

Có bao nhiêu số phức z= x+yi ( x , y thuộc Z) thỏa mãn: | z- 1-i | lớn hơn bằng 2 và | z^2 -z + 1- i | bé hơn bằng 4 ?

Cho số phức z= a+ bi , z khác 0 thỏa mãn1-i / z là số thực và | z- 3i | - | z-3-2i| =2

Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc v1(t) = 2t (m/s). Đi được 12 giây, người lái xe phát hiện chướng ngại

Hình elip được ứng dụng nhiều trong thực tiễn, đặc biệt là kiến trúc xây dựng như đấu trường La Mã, tòa nhà Ellipse Tower Hà Nội

Cho cấp số nhân (un) có số hạng đầu là u1 và công bội là q là số dương thỏa mãn

Tổng n số hạng đầu tiên của một cấp số cộng là Sn = 3n^2 -19n /4 với n thuộc N*

Danh mục