Lời giải
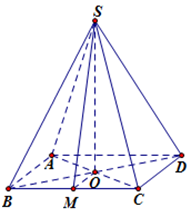
Gọi M là trung điểm của BC, O là giao điểm của AC và BD
Ta có: \(\left\{ \begin{array}{l}BC \bot OM\\BC \bot SO\end{array} \right. \Rightarrow BC \bot \left( {SOM} \right)\)
\( \Rightarrow \left( {\widehat {\left( {SBC} \right),\;\left( {ABCD} \right)}} \right) = \left( {\widehat {SM,\;OM}} \right) = \widehat {SMO} = 45^\circ \)
Do \(AC = 2a \Rightarrow AB = a\sqrt 2 \)
\( \Rightarrow OM = \frac{{a\sqrt 2 }}{2} \Rightarrow SO = OM = \frac{{a\sqrt 2 }}{2}\).
Ta có: SABCD = 2a2
\( \Rightarrow {V_{S.ABCD}} = \frac{1}{3}SO\,.\,{S_{ABCD}} = \frac{1}{3}\,.\,\frac{{a\sqrt 2 }}{2}\,.\,2{a^2} = \frac{{{a^3}\sqrt 2 }}{3}\).