Câu hỏi:
12/03/2024 43Cho hình bình hành ABCD và S nằm ngoài (ABCD), O là giao điểm của AC và BD. M là trung điểm cạnh SC. Trong các khẳng định sau, khẳng định sai là
A. MO // SA;
B. 4 điểm M, O, S và A đồng phẳng;
C. Giao tuyến của (SAB) và (MBD) là Bx trong đó Bx // SA // MO;
D. (MBD) ∩ (SAC) = MD.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
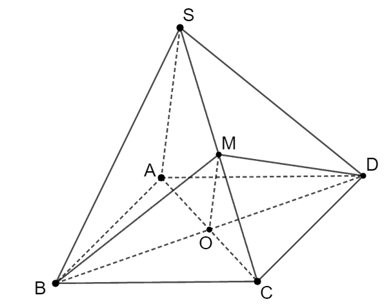
M và O là trung điểm của SC và AC nên OM là đường trung bình của tam giác SAC.
⇒ SA // MO và 4 điểm S, A, M, O đồng phẳng
⇒ A và B đúng.
Ta có:
⇒ (MBD) ∩ (SAB) = Bx // SA // MO.
⇒ C đúng.
Vậy khẳng định sai là D.
Đáp án đúng là: D

M và O là trung điểm của SC và AC nên OM là đường trung bình của tam giác SAC.
⇒ SA // MO và 4 điểm S, A, M, O đồng phẳng
⇒ A và B đúng.
Ta có:
⇒ (MBD) ∩ (SAB) = Bx // SA // MO.
⇒ C đúng.
Vậy khẳng định sai là D.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tứ diện ABCD. Gọi M và N theo thứ tự là trung điểm của AD và AC, G là trọng tâm tam giác BCD. Giao tuyến của hai mặt phẳng (GMN) và (BCD) là đường thẳng
Cho tứ diện ABCD. Gọi M và N theo thứ tự là trung điểm của AD và AC, G là trọng tâm tam giác BCD. Giao tuyến của hai mặt phẳng (GMN) và (BCD) là đường thẳng
Câu 2:
Cho hình thoi ABCD và S nằm ngoài (ABCD). Lấy điểm E trên SA sao cho 2SE = EA; Lấy điểm F trên SB sao cho 2SF = FB. Điểm H nằm trên cạnh SC không trùng với S. Giao tuyến của (EFH) và (SCD) là
Cho hình thoi ABCD và S nằm ngoài (ABCD). Lấy điểm E trên SA sao cho 2SE = EA; Lấy điểm F trên SB sao cho 2SF = FB. Điểm H nằm trên cạnh SC không trùng với S. Giao tuyến của (EFH) và (SCD) là
Câu 3:
Cho hình bình hành ABCD và S nằm ngoài (ABCD). Giao tuyến của hai mặt phẳng (SAB) và (SCD) là một đường thẳng song song với đường thẳng
Cho hình bình hành ABCD và S nằm ngoài (ABCD). Giao tuyến của hai mặt phẳng (SAB) và (SCD) là một đường thẳng song song với đường thẳng
Câu 4:
Cho tứ diện ABCD và ba điểm P, Q, R lần lượt trên cạnh AB, CD và BC. Biết rằng PR // AC. Giao điểm S của mp(PQR) và cạnh AD là
Cho tứ diện ABCD và ba điểm P, Q, R lần lượt trên cạnh AB, CD và BC. Biết rằng PR // AC. Giao điểm S của mp(PQR) và cạnh AD là
Câu 6:
Cho hình bình hành ABCD và S nằm ngoài (ABCD). Giao tuyến của hai mặt phẳng (SAB) và (SCD) là
Cho hình bình hành ABCD và S nằm ngoài (ABCD). Giao tuyến của hai mặt phẳng (SAB) và (SCD) là
Câu 7:
Cho tứ diện ABCD. M và N là trung điểm của AD và AC. G là trọng tâm tam giác BCD. Giao tuyến của 2 mặt phẳng (GMN) và (BCD) là đường thẳng
Cho tứ diện ABCD. M và N là trung điểm của AD và AC. G là trọng tâm tam giác BCD. Giao tuyến của 2 mặt phẳng (GMN) và (BCD) là đường thẳng
Câu 8:
Cho hình thoi ABCD và S nằm ngoài (ABCD). O là giao điểm của AC và BD. E và F lần lượt là trung điểm của CD và AE. Giao tuyến của (SFO) và (SCD) là
Câu 9:
Cho hình bình hành ABCD và điểm S nằm ngoài (ABCD). E là một điểm bất kì thuộc cạnh SA. Giao tuyến của mặt phẳng (ECD) và (SAB) là
Cho hình bình hành ABCD và điểm S nằm ngoài (ABCD). E là một điểm bất kì thuộc cạnh SA. Giao tuyến của mặt phẳng (ECD) và (SAB) là
Câu 10:
Cho hình chóp S. ABCD có đáy là hình thang với các cạnh đáy là AB và CD. M và N là trung điểm AD và BC. G là trọng tâm tam giác SAB. Giao tuyến của (SAB) và (MNG) là:
Cho hình chóp S. ABCD có đáy là hình thang với các cạnh đáy là AB và CD. M và N là trung điểm AD và BC. G là trọng tâm tam giác SAB. Giao tuyến của (SAB) và (MNG) là:


