Câu hỏi:
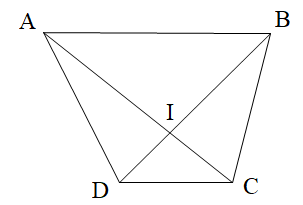
25/01/2024 82Cho hình bình hành ABCD như hình vẽ.
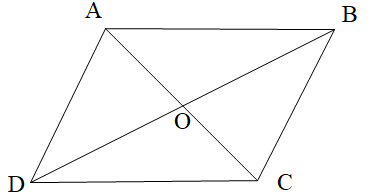
Chọn phương án đúng.
A. ^ABC và ^ADC là hai góc kề bù;
B. ^AOB và ^BOC là hai góc so le trong;
C. ^BAD và ^ADC là hai góc đồng vị;
D. ^AOB và ^DOC là hai góc đối đỉnh.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
^ABC và ^ADC là hai góc kề bù là phát biểu sai vì hai góc này không chung đỉnh.
^AOB và ^BOC là hai góc so le trong là phát biểu sai, vì ^AOB và ^BOC là hai góc kề bù;
^BAD và ^ADC là hai góc đồng vị là phát biểu sai, vì ^BAD và ^ADC là hai góc trong cùng phía.
^AOB và ^DOC là hai góc đối đỉnh là phát biểu đúng, chọn phương án D.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 4:
Cho ^mOn và ^nOp là hai góc kề bù. Biết ^mOn=124∘ và Ot là tia phân giác của góc nOp. Số đo góc mOt là:
Câu 5:
Cho định lí: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” và hình vẽ.
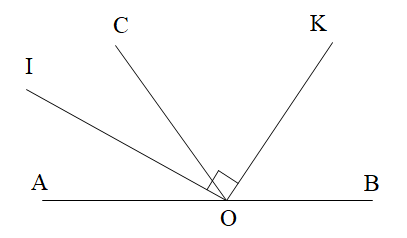
Kết luận của định lí là:
Câu 6:
Cho các phát biểu sau:
(1) Tổng số đo hai góc kề nhau bằng 180o;
(2) Hai góc bằng nhau thì đối đỉnh;
(3) Hai đường thẳng song song thì cắt nhau;
(4) Hai góc kề bù có tổng số đo bằng 180o;
(5) Nếu NH = NK thì N là trung điểm của HK.
Có bao nhiêu phát biểu đúng?
Câu 9:
Cho ba đường thẳng phân biệt a, b và c, biết c // a và c // b. Kết luận nào đúng:
Câu 10:
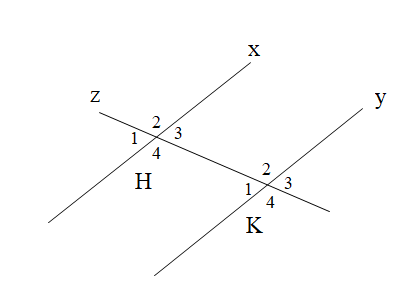
Biết một cặp góc so le trong ^A4=^B2=110∘. Tính số đo của cặp góc so le trong còn lại:
Câu 11:
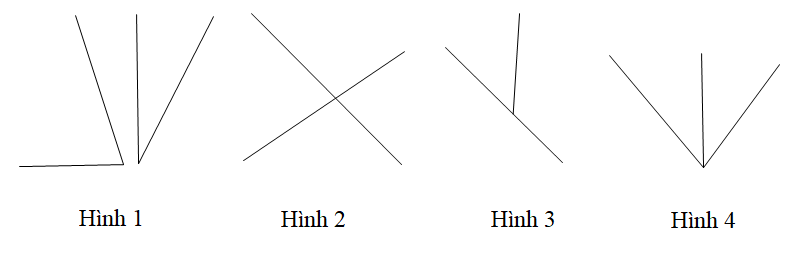
“Nếu hai góc đối đỉnh thì hai góc đó bằng nhau”
Hình minh họa nội dung định lí trên là
Câu 13:
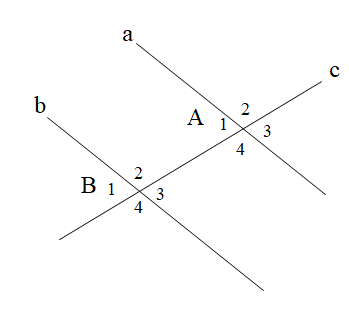
Hai đường thẳng mn và m’n’ cắt nhau tại điểm O. Góc đối đỉnh của ^mOn′ là:
Câu 14:
Cho ^mOn và ^nOp là hai góc kề bù. Biết ^mOn=124∘ và Ot là tia phân giác của góc nOp. Số đo góc mOt là:
Câu 15:
Cho hình bình hành ABCD như hình vẽ. Biết IJ // DC và ^JOC=34∘.
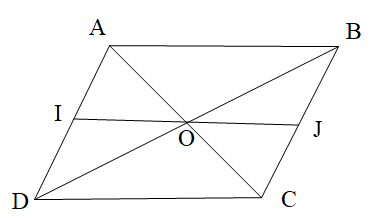
Số đo góc OCD là: