Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Gọi M, N, P, Q lần lượt là trung điểm

Luyện tập 1 trang 7 Chuyên đề Toán 11: Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Xác định ảnh của các điểm N, P, C, A, M qua phép tịnh tiến theo vectơ 

Trả lời

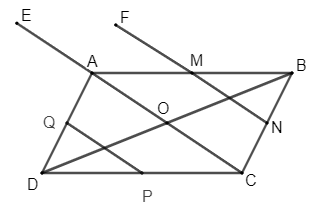
+ Vì M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC, suy ra MN // AC và MN =  AC. Do đó, $\overrightarrow{NM}=\frac{1}{2}\overrightarrow{CA}$  (1).

Vì O là giao điểm của hai đường chéo AC và BD của hình bình hành ABCD nên O là trung điểm của AC, do đó OA =$\frac{1}{2}$ AC. Suy ra$\overrightarrow{OA}=\frac{1}{2}\overrightarrow{CA}$ (2).

Từ (1) và (2) suy ra $\overrightarrow{NM}=\overrightarrow{OA}$  (3).

Vậy ảnh của điểm N qua phép tịnh tiến theo vectơ $\overrightarrow{OA}$  là điểm M.

+ Vì P và Q lần lượt là trung điểm của CD và DA nên PQ là đường trung bình của tam giác ADC, suy ra PQ // AC và PQ =  $\frac{1}{2}$AC. Do đó, $\overrightarrow{PQ}=\frac{1}{2}\overrightarrow{CA}$  (4)

Từ (2) và (4) suy ra $\overrightarrow{PQ}=\overrightarrow{OA}$.

Vậy ảnh của điểm P qua phép tịnh tiến theo vectơ $\overrightarrow{OA}$  là điểm Q.

+ Vì O là trung điểm của AC nên $\overrightarrow{CO}=\overrightarrow{OA}$ .

Vậy ảnh của điểm C qua phép tịnh tiến theo vectơ $\overrightarrow{OA}$   là điểm O.

+ Lấy điểm E đối xứng với điểm O qua điểm A, khi đó A là trung điểm của OE.

Suy ra $\overrightarrow{AE}=\overrightarrow{OA}$ ->.

Vậy ảnh của điểm A qua phép tịnh tiến theo vectơ $\overrightarrow{OA}$  là điểm E.

+ Lấy điểm F đối xứng với điểm N qua điểm M, khi đó M là trung điểm của NF.

Suy ra $\overrightarrow{NM}=\overrightarrow{MF}$  (5).

Từ (3) và (5) suy ra $\overrightarrow{MF}=\overrightarrow{OA}$ .

Vậy ảnh của điểm M qua phép tịnh tiến theo vectơ $\overrightarrow{OA}$.

Xem thêm các bài giải Chuyên đề Toán lớp 11 Cánh diều hay, chi tiết khác:

Bài 1: Phép dời hình

Bài 2: Phép đồng dạng

Bài 1: Một vài yếu tố của lí thuyết đồ thị. Đường đi Euler và đường đi Hamilton

Bài 2: Một vài ứng dụng của lí thuyết đồ thị

Bài 1: Một số nội dung cơ bản về vẽ kĩ thuật

Bài 2: Đọc và vẽ bản vẽ kĩ thuật đơn giản