Cho hình bình hành ABCD. Các đường phân giác của các góc lần lượt cắt nhau tại E, F, G, H. Chứng minh: EFGH là hình chữ nhật.

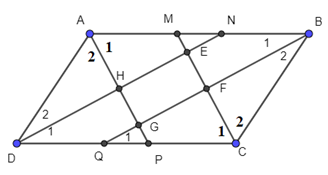
a) Gọi M, N, P, Q lần lượt là giao điểm của các đường phân giác với các cạnh của hình bình hành.

Ta có: $\widehat{D_1}=\widehat{D_2}=\frac{\widehat{ADC}}{2}$  (DN là phân giác $\widehat{ADC}$ )

$\widehat{B_1}=\widehat{B_2}=\frac{\widehat{ABC}}{2}$ (BQ là phân giác $\widehat{ABC}$)

Mà $\widehat{ADC}=\widehat{ABC}$(hai góc đối của hình bình hành ABCD)

⇒ $\widehat{D_1}=\widehat{B_1}$

Vì ABCD là hình bình hành AB // CD ⇒ $\widehat{Q_1}=\widehat{B_1}$ (hai góc so le trong)

⇒ $\widehat{Q_1}=\widehat{D_1}$

Mà hai góc ở vị trí đồng vị

⇒ DN // BQ hay HE // GF

Ta có: $\widehat{A_1}=\widehat{A_2}=\frac{\widehat{DAB}}{2}$  (AP là phân giác $\widehat{DAB}$)

$\widehat{C_1}=\widehat{C_2}=\frac{\widehat{DCB}}{2}$(CM là phân giác $\widehat{DCB}$ )

Mà $\widehat{DAB}=\widehat{DCB}$ (hai góc đối của hình bình hành ABCD)

⇒ $\widehat{A_1}=\widehat{C_1}$

Vì ABCD là hình bình hành AB // CD ⇒ $\widehat{A_1}=\widehat{QPG}$  (hai góc so le trong)

⇒ $\widehat{C_1}=\widehat{QPB}$

⇒ AP //DM hay GH // EF

Xét tứ giác EFGH có:

HE // GF (cmt)

GH // EF (cmt)

⇒ EFGH là hình bình hành (1)

Xét tam giác BFC, có: $\widehat{B_2}+\widehat{C_2}=\frac{\widehat{ABC}}{2}+\frac{\widehat{BCD}}{2}=\frac{\widehat{ABC}+\widehat{BCD}}{2}$

Mà $\widehat{ABC}+\widehat{BCD}$ = 180°(hai góc trong cùng phía bù nhau)

⇒ $\widehat{B_2}+\widehat{C_2}=\frac{180°}{2}=90°$ ⇒ $\widehat{BFC}=180°-\left(\widehat{B_2}+\widehat{C_2}\right)=90°$

⇒ $\widehat{EFG}$ = 90°(2)

Từ (1) và (2) suy ra tứ giác EFGH là hình chữ nhật.