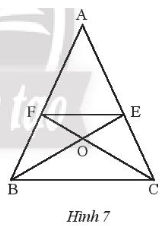
Cho Hình 7, biết AB = AC và BE là tia phân giác của góc ABC; CF là tia phân giác của góc ACB. Chứng minh rằng

Bài 4 trang 49 SBT Toán 7 Tập 2:

Cho Hình 7, biết AB = AC và BE là tia phân giác của $\widehat{ABC}$; CF là tia phân giác của $\widehat{ACB}$. Chứng minh rằng:

a) ΔABE = ΔACF;

b) Tam giác OEF cân.

Trả lời

Chứng minh (Hình 7):

a) Vì AB = AC (giả thiết) nên tam giác ABC cân tại A.

Suy ra $\widehat{ABC}=\widehat{ACB}$ (tính chất)          (1)

Ta có BE là tia phân giác của $\widehat{ABC}$ (giả thiết)

Nên $\widehat{ABE}=\widehat{EBC}=\frac{1}{2}\widehat{ABC}$ (tính chất tia phân giác) (2)

Lại có CF là tia phân giác của $\widehat{ACB}$ (giả thiết)

Nên $\widehat{ACF}=\widehat{FCB}=\frac{1}{2}\widehat{ACB}$ (tính chất tia phân giác) (3)

Từ (1), (2), (3) suy ra $\widehat{ACF}=\widehat{FCB}=\widehat{ABE}=\widehat{EBC}$.

Xét ΔABE và ΔACF có:

$\widehat{A}$ là góc chung,

AB = BC (giả thiết),

$\widehat{ABE}=\widehat{ACF}$ (chứng minh trên).

Do đó ΔABE = ΔACF (g.c.g).

Vậy ΔABE = ΔACF.

b) Vì ΔABE = ΔACF (chứng minh câu a).

Nên BE = CF (hai cạnh tương ứng).

Xét ΔOBC có $\widehat{OBC}=\widehat{OCB}$ (do $\widehat{EBC}=\widehat{FCB}$)

Do đó ΔOBC cân tại O.

Suy ra OB = OC (tính chất tam giác cân).

Ta có: BE = OB + OE, CF = OC + OF.

Mà BE = CF, OB = OC (chứng minh trên).

Suy ra OE = OF

Do đó ΔOEF cân tại O.

Vậy tam giác OEF cân tại O.

Xem thêm lời giải sách bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 7

Bài 1: Góc và cạnh của một tam giác

Bài 2: Tam giác bằng nhau

Bài 3: Tam giác cân

Bài 4: Đường vuông góc và đường xiên

Bài 5: Đường trung trực của một đoạn thẳng