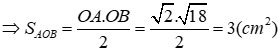Cho hệ phương trình : x + my = 2; 2x + 4y = 3 a) Giải hệ phương trình khi m = 3 b) Tìm m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn điều kiện x và y là hai số đối nhau .
117
07/05/2024
1) Cho hệ phương trình : 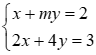
a) Giải hệ phương trình khi m = 3
b) Tìm m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn điều kiện x và y là hai số đối nhau .
2) Cho hàm số 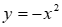 có đồ thị là parabol (P) và hàm số y = x - 2 có đồ thị là đường thẳng (d). Gọi A và B là giao điểm của (d) với (P). Tính diện tích tam giác OAB.
có đồ thị là parabol (P) và hàm số y = x - 2 có đồ thị là đường thẳng (d). Gọi A và B là giao điểm của (d) với (P). Tính diện tích tam giác OAB.
Trả lời
1) a) Khi \(m = 3 \Rightarrow \left\{ \begin{array}{l}x + 3y = 2\\2x + 4y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{1}{2}\\y = \frac{1}{2}\end{array} \right.\)
\(b)\left\{ \begin{array}{l}x + my = 2\\2x + 4y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x + 2my = 4\\2x + 4y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = \frac{1}{{2m - 4}}\\x = \frac{{3 - \frac{2}{{m - 2}}}}{2} = \frac{{2\left( {3m - 8} \right)}}{{m - 2}}\end{array} \right.\)
Để \(x,y\)đối nhau thì :
\( \Rightarrow \frac{{2\left( {3m - 8} \right)}}{{m - 2}} = \frac{{ - 1}}{{2m - 4}} \Leftrightarrow \left( {6m - 16} \right).2 = - 1 \Leftrightarrow 12m = 31 \Leftrightarrow m = \frac{{31}}{{12}}\)
2) Hoành độ \(A,B\)là nghiệm hệ \( - {x^2} = x - 2 \Leftrightarrow {x^2} + x - 2 = 0\)
\( \Rightarrow \left[ \begin{array}{l}{x_A} = 1 \Rightarrow {y_A} = - 1\\{x_B} = - 2 \Rightarrow {y_B} = - 4\end{array} \right. \Rightarrow A\left( {1; - 1} \right);B\left( { - 2; - 4} \right),O\left( {0;0} \right)\)
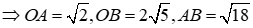
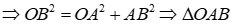 vuông tại A
vuông tại A
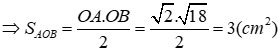
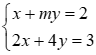
![]() có đồ thị là parabol (P) và hàm số y = x - 2 có đồ thị là đường thẳng (d). Gọi A và B là giao điểm của (d) với (P). Tính diện tích tam giác OAB.
có đồ thị là parabol (P) và hàm số y = x - 2 có đồ thị là đường thẳng (d). Gọi A và B là giao điểm của (d) với (P). Tính diện tích tam giác OAB.