Cho hàm số y = f( x)  có đạo hàm là hàm số y = f’(x)  trên R. Biết rằng hàm số y = f ' (x – 2) + 2  có đồ thị như hình vẽ bên dưới. Hàm số y = f( x)  nghịch biến trên khoảng nào?

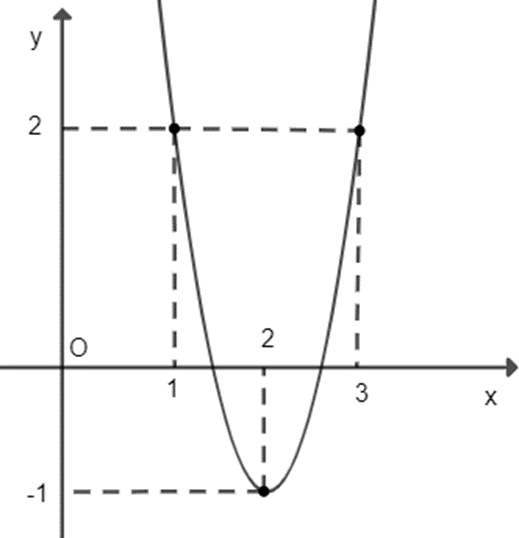
A. (−∞; 2);

B. (−1; 1);

C. \(\left( {\frac{3}{2};\frac{5}{2}} \right)\);

D. (2; +∞).

Đáp án đúng là: B

Dựa vào đồ thị (C) ta có:

f '(x – 2) + 2 < 2, với mọi x ∈ (1; 3)

⇔ f '(x – 2) < 0, với mọi x ∈ (1; 3).

Đặt t = x – 2 thì

f '(t) < 0, với mọi t ∈ (−1; 1)

Vậy hàm số nghịch biến trên khoảng (−1; 1).