Cho hai vectơ a và b không cùng phương. Chứng minh rằng: |a| - |b| < |a + b| < |a| + |b|

Bài 4.7 trang 50 SBT Toán 10 Tập 1: Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ không cùng phương. Chứng minh rằng:

$\left|\overrightarrow{a}\right|-\left|\overrightarrow{b}\right|<\left|\overrightarrow{a}+\overrightarrow{b}\right|<\left|\overrightarrow{a}\right|+\left|\overrightarrow{b}\right|$

Trả lời

Giả sử ba điểm A, B, C thoả mãn: $\overrightarrow{a}=\overrightarrow{AB},\overrightarrow{b}=\overrightarrow{BC}$ 

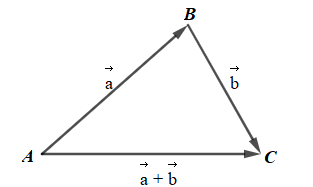
Khi đó ta có: $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$ (quy tắc ba điểm)

Do đó:

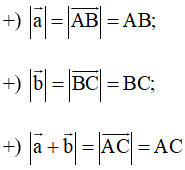
Mặt khác: xét tam giác ABC, theo bất đẳng thức trong tam giác ta có:

AB – BC < AC < AB + BC

Hay $\left|\overrightarrow{a}\right|-\left|\overrightarrow{b}\right|<\left|\overrightarrow{a}+\overrightarrow{b}\right|<\left|\overrightarrow{a}\right|+\left|\overrightarrow{b}\right|$ 

Vậy $\left|\overrightarrow{a}\right|-\left|\overrightarrow{b}\right|<\left|\overrightarrow{a}+\overrightarrow{b}\right|<\left|\overrightarrow{a}\right|+\left|\overrightarrow{b}\right|.$

Xem thêm các bài giải SBT Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 3

Bài 7: Các khái niệm mở đầu

Bài 8: Tổng và hiệu của hai vectơ

Bài 9: Tích của một vectơ với một số

Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 11: Tích vô hướng của hai vectơ