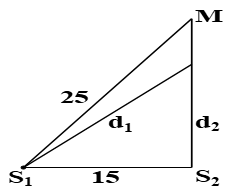
Cho hai nguồn sóng kết hợp \({{\rm{S}}_1}{{\rm{S}}_2}\) trên mặt chất lỏng cách nhau 15 cm, dao động với phương trình là \({{\rm{u}}_{{{\rm{S}}_1}}} = {{\rm{u}}_{{{\rm{S}}_2}}} = 2{\rm{cos}}10{\rm{\pi t\;}}\left( {{\rm{cm}}} \right)\) (t tính bằng giây). Tốc độ truyền sóng trên mặt chất lỏng là \(10{\rm{\;cm}}/{\rm{s}}\). Coi biên độ dao động không đổi khi truyền đi. Điểm \({\rm{M}}\) nằm trên đường thẳng vuông góc với \({{\rm{S}}_1}{{\rm{S}}_2}\) tại \({{\rm{S}}_2}\) cách \({{\rm{S}}_1}\) là \(25{\rm{\;cm}}\). Khoảng cách giữa hai điểm gần \({{\rm{S}}_2}\) nhất và xa \({{\rm{S}}_2}\) nhất có tốc độ dao động cực đại bằng \(20{\rm{\pi }}\sqrt 2 {\rm{\;}}\left( {{\rm{cm}}/{\rm{s}}} \right)\) trên đoạn \({{\rm{S}}_2}{\rm{M}}\) là

D. \(16,1{\rm{\;cm}}\)

\(\lambda = v.\frac{{2\pi }}{\omega } = 10.\frac{{2\pi }}{{10\pi }} = 2cm\)

\(A = \frac{{{v_{\max }}}}{\omega } = \frac{{20\pi \sqrt 2 }}{{10\pi }} = 2\sqrt 2 cm = \frac{{{A_b}}}{{\sqrt 2 }}\)

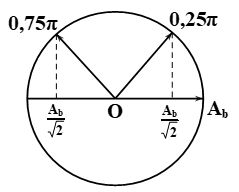
\( \Rightarrow \)pha biên độ lệch \(0,25\pi \) hoặc \(0,75\pi \) \( \Rightarrow \)bậc có dạng ,25 hoặc ,75

\(\frac{{M{S_1} - M{S_2}}}{\lambda } < k < \frac{{{S_1}{S_2}}}{\lambda } \Rightarrow \frac{{25 - \sqrt {{{25}^2} - {{15}^2}} }}{2} < k < \frac{{15}}{2} \Rightarrow 2,5 < k < 7,5\)

\({d_1} - {d_2} = k\lambda \Rightarrow \sqrt {d_2^2 + {{15}^2}} - {d_2} = k.2 \Rightarrow \left\{ \begin{array}{l}k = 2,75 \Rightarrow {d_2} \approx 17,7cm\\k = 7,25 \Rightarrow {d_2} \approx 0,5cm\end{array} \right.\)

\(\Delta {d_2} = 17,7 - 0,5 = 17,2cm\). Chọn A