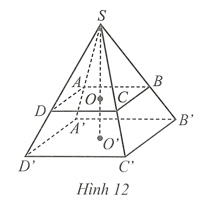
Cho hai hình chóp tứ giác đều S.ABCD và S.A'B'C'D' lần lượt có chiều cao SO và SO'. Biết AB = 2a, A'B' = 3a, SO = 2b, SO' =3b (Hình 12). Tính tỉ số thể tích của hình chóp tứ giác đều S.ABCD v
35
30/07/2024
Cho hai hình chóp tứ giác đều S.ABCD và S.A'B'C'D' lần lượt có chiều cao SO và SO'. Biết AB = 2a, A'B' = 3a, SO = 2b, SO' =3b (Hình 12). Tính tỉ số thể tích của hình chóp tứ giác đều S.ABCD và S.A'B'C'D'. Biết rằng a và b cùng đơn vị đo.
Trả lời
Lời giải
Thể tích của hình chóp tứ giác đều S.ABCD là:
\(V = \frac{1}{3}.{S_{ABCD}}.SO = \frac{1}{3}.\left( {2a.2a} \right).2b = \frac{{8{a^2}b}}{3}{\rm{\;}}\) (đơn vị thể tích).
Thể tích của hình chóp tứ giác đều S.A’B’C’D’ là:
\(V' = \frac{1}{3}.{S_{A'B'C'D'}}.SO' = \frac{1}{3}.\left( {3a.3a} \right).3b = 9{a^2}b{\rm{\;}}\) (đơn vị thể tích).
Tỉ số thể tích của hình chóp tứ giác đều S.ABCD và S.A’B’C’D’ là:
\(\frac{V}{{V'}} = \frac{{8{a^2}b}}{3}:\left( {9{a^2}b} \right) = \frac{8}{{27}}\).