Cho hai hàm số f (x) = ax^3 + bx^2 + cx − 2 và g (x) = dx^2 + ex + 2

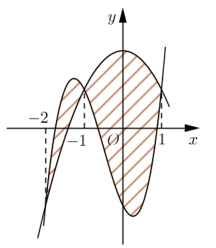
Trả lời

Phương trình hoành độ giao điểm của đồ thị f (x) và g (x) là:

ax³ + bx² + cx − 2 = dx² + ex + 2

Û ax³ + (b − d)x² + (c − e)x − 4 = 0 (1)

Vì phương trình (1) có các nghiệm −2; −1; 1 nên: 

$\left\{\begin{array}{l}a.{\left(-2\right)}^3+\left(b-d\right).{\left(-2\right)}^2+\left(c-e\right).\left(-2\right)-4=0\\ a.{\left(-1\right)}^3+\left(b-d\right).{\left(-1\right)}^2+\left(c-e\right).\left(-1\right)-4=0\\ a.1^3+\left(b-d\right).1^2+\left(c-e\right).1-4=0\end{array}\right.$

$\iff \left\{\begin{array}{l}-8a+4\left(b-d\right)-2\left(c-e\right)-4=0\\ -a+\left(b-d\right)-\left(c-e\right)-4=0\\ a+\left(b-d\right)+\left(c-e\right)-4=0\end{array}\right.$

$\iff \left\{\begin{array}{l}3a-3\left(b-d\right)+6=0\\ 2\left(b-d\right)-8=0\\ a+\left(b-d\right)+\left(c-e\right)-4=0\end{array}\right.$

$\iff \left\{\begin{array}{l}a=b-d-2\\ b-d=4\\ a+\left(b-d\right)+\left(c-e\right)=4\end{array}\right.$

$\iff \left\{\begin{array}{l}a=2\\ b-d=4\\ c-e=4-a-\left(b-d\right)\end{array}\right.\iff \left\{\begin{array}{l}a=2\\ b-d=4\\ c-e=-2\end{array}\right.$

Diện tích hình phẳng cần tìm là: 

$S=\underset{-2}{\overset{-1}{\int }}\left[f\left(x\right)-g\left(x\right)\right]dx+\underset{-1}{\overset{1}{\int }}\left[g\left(x\right)-f\left(x\right)\right]dx$

$=\underset{-2}{\overset{-1}{\int }}\left[a{x}^3+\left(b-d\right)x^2+\left(c-e\right)x-4\right]dx+\underset{-1}{\overset{1}{\int }}\left[-a{x}^3-\left(b-d\right)x^2-\left(c-e\right)x+4\right]dx$

$=\underset{-2}{\overset{-1}{\int }}\left[2x^3+4x^2-2x-4\right]dx+\underset{-1}{\overset{1}{\int }}\left[-2x^3-4x^2+2x+4\right]dx$

$={\left.\left(\frac{x^4}{2}+\frac{4x^3}{3}-x^2-4x\right)\right|}_{-2}^{-1}+{\left.\left(-\frac{x^4}{2}-\frac{4x^3}{3}+x^2+4x\right)\right|}_{-1}^1$

$=\frac{{\left(-1\right)}^4}{2}+\frac{4.{\left(-1\right)}^3}{3}-{\left(-1\right)}^2-4.\left(-1\right)-\frac{{\left(-2\right)}^4}{2}-\frac{4.{\left(-2\right)}^3}{3}+{\left(-2\right)}^2-4.\left(-2\right)$

$-\frac{1^4}{2}-\frac{4.1^3}{3}+1^2+4.1+\frac{{\left(-1\right)}^4}{2}+\frac{4.{\left(-1\right)}^3}{3}-{\left(-1\right)}^2-4.\left(-1\right)$

$=\frac{1}{2}-\frac{4}{3}-1+4-8+\frac{32}{3}+4+8-\frac{1}{2}-\frac{4}{3}+1+4+\frac{1}{2}-\frac{4}{3}-1+4$

$=\frac{37}{6}$