Cho hai hàm số f(x)={2xn\^e′u0≤x≤121n\^e′u12<x≤1 và g(x)={xn\^e′u0≤x≤121n\^e′u12<x≤1 với đồ thị tương ứng như Hình 5.7.
Xét tính liên tục của các hàm số f(x) và g(x) tại điểm x=12 và nhận xét về sự khác nhau giữa hai đồ thị.
Lời giải:
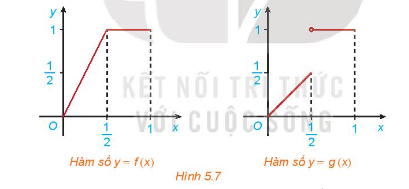
+) Hàm số f(x)={2xn\^e′u0≤x≤121n\^e′u12<x≤1.
Hàm số f(x) xác định trên [0; 1], do đó x=12 thuộc tập xác định của hàm số.
Ta có: lim; \mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ - }} \left( {2x} \right) = 2 \cdot \frac{1}{2} = 1.
Suy ra \mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ - }} f\left( x \right) = 1, do đó \mathop {\lim }\limits_{x \to \frac{1}{2}} f\left( x \right) = 1
Mà f\left( {\frac{1}{2}} \right) = 2 \cdot \frac{1}{2} = 1 nên \mathop {\lim }\limits_{x \to \frac{1}{2}} f\left( x \right) = f\left( {\frac{1}{2}} \right).
Vậy hàm số f(x) liên tục tại x = \frac{1}{2}.
+) Hàm số g\left( x \right) = \left\{ \begin{array}{l}x\,\,\,n\^e 'u\,\,0 \le x \le \frac{1}{2}\\1\,\,\,\,n\^e 'u\,\,\frac{1}{2} < x \le 1\end{array} \right..
Hàm số g(x) xác định trên [0; 1], do đó x = \frac{1}{2} thuộc tập xác định của hàm số.
Ta có: \mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ - }} g\left( x \right) = \mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ - }} x = \frac{1}{2}; \mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ + }} g\left( x \right) = \mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ + }} 1 = 1
Suy ra \mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ + }} g\left( x \right) \ne \mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ - }} g\left( x \right).
Vậy không tồn tại giới hạn của hàm số g(x) tại x = \frac{1}{2}, do đó hàm số g(x) gián đoạn tại x = \frac{1}{2}.
+) Quan sát Hình 5.7 ta thấy, đồ thị của hàm số y = f(x) là đường liền trên (0; 1), còn đồ thị của hàm số y = g(x) trên (0; 1) là các đoạn rời nhau.