Cho hai đường tròn (O) và (O’) tiếp xúc trong tại A. Qua A vẽ dây AB, AC của đường tròn (O), chúng cắt (O’) theo thứ tự tại D và E. Chứng minh BC // DE.

Trả lời

Lời giải

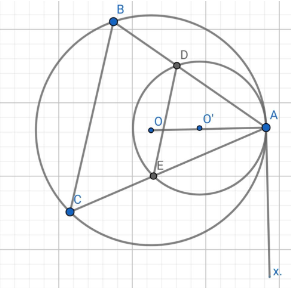
Vì (O) và (O’) tiếp xúc trong tại A.

Suy ra A thuộc đường nối tâm OO’.

Qua A, vẽ tiếp tuyến Ax chung của hai đường tròn (O) và (O’).

Xét đường tròn (O’), có: \(\widehat {EAx} = \widehat {EDA} = \frac{1}{2}\)sđ     (1)

Xét đường tròn (O), có: \(\widehat {CAx} = \widehat {CBA} = \frac{1}{2}\)sđ       (2)

Ta có \(\widehat {EAx} = \widehat {CAx}\)      (3)

Từ (1), (2), (3), suy ra \(\widehat {CBA} = \widehat {EDA}\).

Mà hai góc này ở vị trí đồng vị.

Vậy BC // DE (điều phải chứng minh).