Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM = ON, OA > OM

Bài 4.30 trang 86 Toán 7 Tập 1: Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM = ON, OA > OM. Chứng minh rằng:

a) $\Delta OAN=\Delta OBM;$

b) $\Delta AMN=\Delta BNM.$

Trả lời

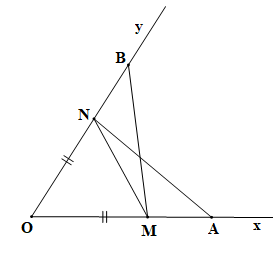
a) Xét tam giác OAN và tam giác OBM có:

OA = OB (theo giả thiết);

$\widehat{AOB}$ là góc chung;

ON = OM (theo giả thiết).

Vậy $\Delta OAN=\Delta OBM$ (c.g.c).

b) Do B, N cùng nằm trên tia Oy, OA = OB, OM = ON và OA > OM (theo giả thiết) nên OB > ON, khi đó OB = ON + NB suy ra NB = OB – ON.

Do A, M cùng nằm trên tia Ox, OA > OM (theo giả thiết) nên OA = OM + MA suy ra MA = OA – OM.

Lại có OA = OB, OM = ON (theo giả thiết) nên OA – OM = OB – ON.

Hay MA = NB.

Từ $\Delta OAN=\Delta OBM$ (chứng minh ở câu a) suy ra AN = BM (hai cạnh tương ứng).

Xét tam giác AMN và tam giác BNM có:

AN = BM (chứng minh trên);

MN là cạnh chung;

MA = NB (chứng minh trên).

Vậy $\Delta AMN=\Delta BNM(c.g.c).$

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 15: Các trường hợp bằng nhau của tam giác vuông

Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng

Luyện tập chung trang 86

Bài tập cuối chương 4 trang 87

Bài 17: Thu thập và phân loại dữ liệu

Bài 18: Biểu đồ hình quạt tròn