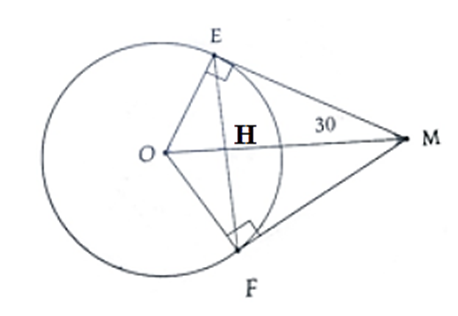
Cho đường tròn tâm O. Từ điểm M nằm ngoài đường tròn, vẽ hai tiếp tuyến ME và MF
Cho đường tròn tâm O. Từ điểm M nằm ngoài đường tròn, vẽ hai tiếp tuyến ME và MF sao cho góc EMO bằng 30 độ. Biết chu vi tam giác MEF là 30 cm. Tính:
a) Độ dài EF.
b) Diện tích tam giác MEF.