Cho đường tròn tâm (O) bán kính OA = 3cm. Dây BC của đường tròn vuông góc với OA
Cho đường tròn tâm (O) bán kính OA = 3cm. Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Tính độ dài BC.
Cho đường tròn tâm (O) bán kính OA = 3cm. Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Tính độ dài BC.
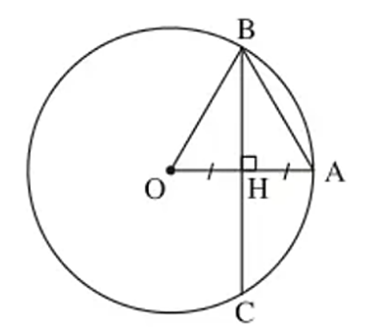
Gọi giao điểm của OA và BC là H
Xét tam giác ABH vuông tại H (do BC vuông góc với OA tại H)
B nằm trên đường tròn (O) nên OB = OA = 3cm
H là trung điểm của OA
nên OH = AH = \(\frac{1}{2}\)OA = 3 : 2 = 1,5 cm
Áp dụng định lí Py–ta–go ta có:
OB2 = BH2 + OH2
⇒ BH2 = OB2 − OH2 = 32 − (1,5)2 = 6,75
⇒ BH = \(\sqrt {6,75} = \frac{{3\sqrt 3 }}{2}\left( {cm} \right)\)
Mặt khác, OA là bán kính và là một phần của đường kính, OA vuông góc với dây cung BC tại H.
Do đó, H là trung điểm của BC
⇒ HB = HC = \(\frac{1}{2}\)BC
⇒ BC = 2HB = \(2.\frac{{3\sqrt 3 }}{2} = 3\sqrt 3 \left( {cm} \right)\).