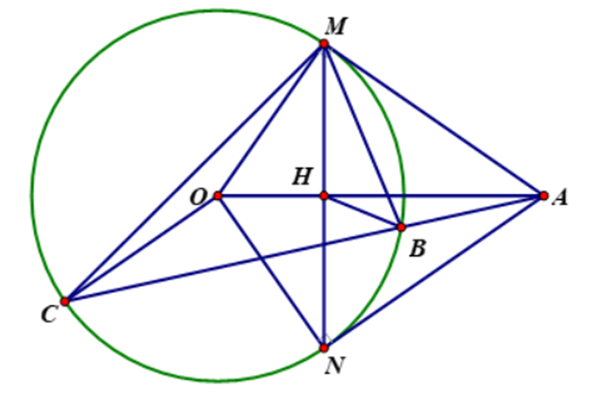
a) \(\widehat {OMA} = \widehat {ONA} = 90^\circ \)(vì AM, AN là tiếp tuyến của (O))

Xét tứ giác OMAN có: \(\widehat {OMA} + \widehat {ONA} = 180^\circ \)

Do đó: OMAN là tứ giác nội tiếp

hay O, M, A, N cùng thuộc 1 đường tròn

b) Xét tam giác AMB và tam giác ACM có:

\(\widehat {MAC}\)là góc chung

\(\widehat {MCA} = \widehat {BMA}\)(góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung)

Suy ra: ∆AMB ∽ ∆ACM (g.g)

⇒ \(\frac{{AM}}{{AC}} = \frac{{AB}}{{AM}}\) hay AM² = AB.AC

c) Ta có: OM = ON = R

MA = NA (tính chất hai tiếp tuyến cắt nhau)

Khi đó OA là trung trực của MN.

Suy ra: OA vuông góc MN

Xét tam giác OMA vuông tại M có đường cao MH, ta cóL

MA² = AH.AO

Mà AM² = AB.AC nên AH.AO = AB.AC

Suy ra: \(\frac{{AB}}{{AO}} = \frac{{AH}}{{AC}}\)

Xét ∆ABH và ∆AOC có:

\(\frac{{AB}}{{AO}} = \frac{{AH}}{{AC}}\)

\(\widehat {OAC}\)là góc chung

⇒ ∆ABH ∽ ∆AOC (c.g.c)

⇒ \(\widehat {AHB} = \widehat {ACO}\)(hai góc tương ứng)

Do đó tứ giác BHOC nội tiếp.