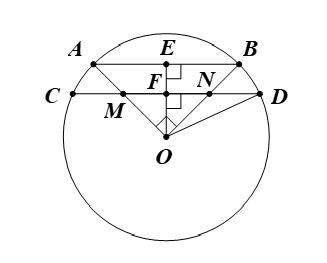
Cho đường tròn (O; R) và hai bán kính OA, OB. Trên các bán kính OA, OB lần lượt lấy các điểm M, N sao cho OM = ON. Vẽ dây CD qua M và N (M nằm giữa C và N).

1) Chứng minh rằng CM = DN.

1) Kẻ OE ⊥ AB và OE cắt CD tại F.

Ta có OA = OB (giả thiết) và OM = ON (giả thiết).

Suy ra $\frac{OM}{OA}=\frac{ON}{OB}$ .

Áp dụng định lí Thales đảo, ta được MN // AB.

Mà OE ⊥ AB.

Do đó OE ⊥ CD tại F.

Suy ra F là trung điểm của CD (quan hệ giữa đường kính và dây cung).

Vì vậy CF = FD.

Ta có OM = ON (giả thiết).

Suy ra ∆OMN cân tại O.

∆OMN cân tại O có OF là đường cao.

Suy ra OF cũng là đường trung tuyến của ∆OMN.

Do đó F là trung điểm MN.

Vì vậy MF = NF.

Ta có CF = FD (chứng minh trên).

Khi đó CM + MF = FN + ND.

Mà MF = NF (chứng minh trên).

Vậy CM = DN.