Cho đường tròn (O;R) và dây cung MN = R căn bậc hai 3. Kẻ OK vuông góc MN
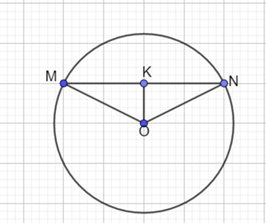
Cho đường tròn (O;R) và dây cung MN = \(R\sqrt 3 \). Kẻ OK vuông góc MN tại K.
a) Tính OK theo r.
b) Tính góc \(\widehat {MOK}\) và góc \(\widehat {MON}\).
c) Tính số đo cung nhỏ, cung lớn MN.