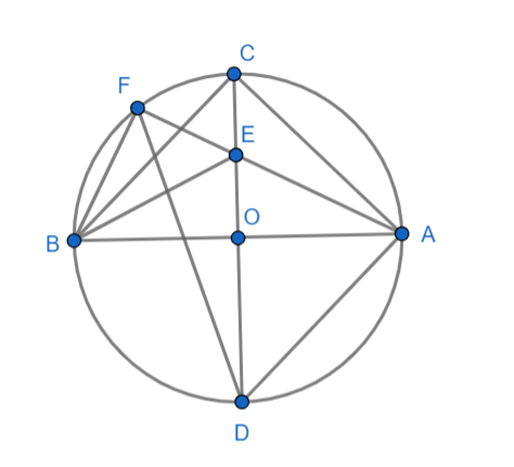
a) Theo giả thiết: CD vuông góc AB nên \(\widehat {EOB} = 90^\circ \)
Lại có: \(\widehat {BFA} = 90^\circ \)(góc nội tiếp chắn nửa đường tròn)
⇒ \[\widehat {EOB} + \widehat {BFA} = 90^\circ + 90^\circ = 180^\circ \]
⇒ OEFB là tứ giác nội tiếp
Vì E là trung điểm OC nên CE = OE = \(\frac{1}{2}OC = \frac{1}{2}R\)
Áp dụng định lý Pytago vào tam giác OBE vuông tại O có:
BE2 = OE2 + OB2
⇒ BE = \(\sqrt {{R^2} + {{\left( {\frac{R}{2}} \right)}^2}} = \frac{{R\sqrt 5 }}{2}\)
Bán kính của đường tròn ngoại tiếp tứ giác OEFB = \(\frac{1}{2}BE = \frac{{R\sqrt 5 }}{4}\)
b) tan\(\widehat {EAO} = \frac{R}{2}:R = \frac{1}{2}\) ⇒ \(\widehat {EAO} \approx 26,565^\circ \)
Lại có: \(\widehat {BCA} = 90^\circ \)(góc nội tiếp chắn nửa đường tròn)
Mà CO vừa là đường cao vừa là đường trung tuyến trong tam giác CBA
Nên tam giác CAB là tam giác vuông cân tại C
⇒ \(\widehat {CBA} = \widehat {CAB} = 45^\circ \)
\(\tan \widehat {EAO}\)= \[\widehat {CAE} = 45^\circ - 26,565^\circ \approx 18,435^\circ \]
\[\tan \widehat {CAE} = \frac{1}{3}\]
Lại có:
Suy ra: \[\tan \widehat {CAE} = \tan \widehat {CDF} = \frac{1}{3}\].