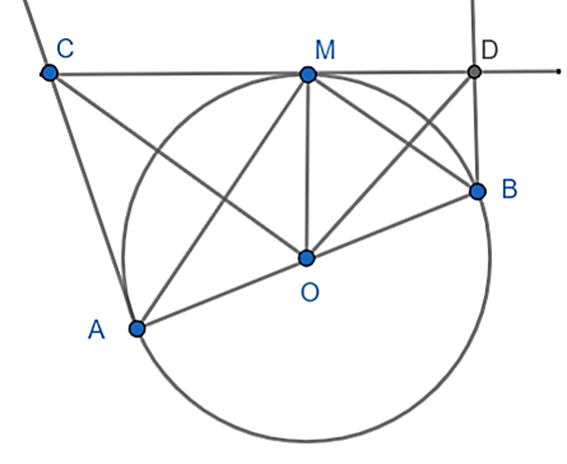
Cho đường tròn (O; R) đường kính AB, M là một điểm bất kì trên đường tròn (M khác A và B) tiếp tuyến cắt tại m cắt hai tiếp tuyến của A và B của đường tròn đã cho tại C và D. Chứng minh rằng: tứ giác AOMC và BOMD nội tiếp; \(\widehat {AOC} = \widehat {AMC} = \widehat {OBM} = \widehat {ODM}\).
Xét tứ giác AOMC có
\(\widehat {OAC} = 90^\circ \) (tiếp tuyến của (O) tại A)
\(\widehat {OMC} = 90^\circ \)(tiếp tuyến của (O) tại M)
⇒ Tứ giác AOMC nội tiếp dường tròn đường kính OC (2 góc đối nhau có tổng =180 độ)
Xét tứ giác BOMD có
\(\widehat {OBD} = 90^\circ \)(tiếp tuyến của (O) tại B)
\(\widehat {OMD} = 90^\circ \)(tiếp tuyến của (O) tại M)
⇒ Tứ giác BOMD nội tiếp đường tròn đường kính OD (2 góc đối nhau có tổng bằng 180 độ)
Ta có : \(\widehat {OBM} = \widehat {AMC}\)(góc tạo bởi tia tiếp tuyến và dây cung, góc nội tiếp cùng chắn cung AM)
\(\widehat {AOC} = \widehat {AMC}\)(góc nội tiếp chắn cung AC của đường tròn ngoại tiếp tứ giác AOMC)
\(\widehat {OBM} = \widehat {ODM}\) (góc nội tiếp chắn cung OM của đường tròn ngoại tiếp tứ giác BOMD)
⇒ \(\widehat {AOC} = \widehat {AMC} = \widehat {OBM} = \widehat {ODM}\).