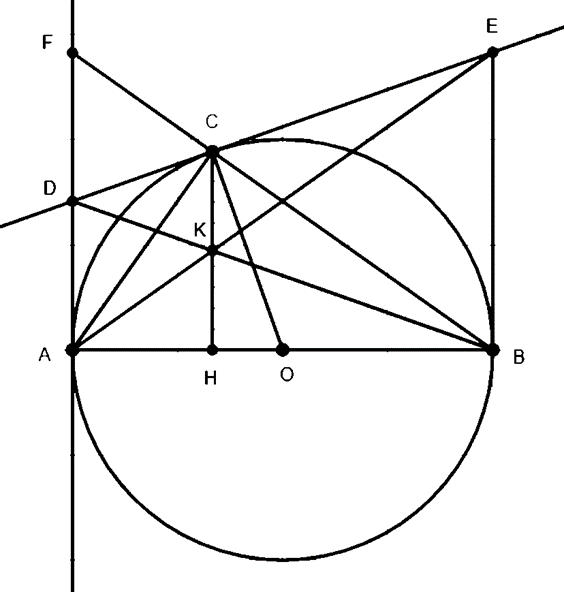
a) \(\widehat {ACB} = 90^\circ \) vì là góc nội tiếp chắn nửa đường tròn nên ΔABC ⊥ C

b) \(\widehat {DCA} = \widehat {CBA}\)

⇒ \(\widehat {DFC} = \widehat {DCF}\) (cùng phụ với 2 góc bằng nhau \(\widehat {FBC} = \widehat {DCA}\))

⇒ ΔDCF cân đỉnh D

⇒ DF = DC (1)

DC = DA (tính chất 2 tiếp tuyến cắt nhau)

Từ (1) và (2) suy ra DF = DA.

c) Ta có: KH // AD theo định lý Ta–lét ta có:

\(\frac{{HK}}{{AD}} = \frac{{BK}}{{BD}}\)

CK // DF ⇒ \(\frac{{CK}}{{DF}} = \frac{{BK}}{{BD}}\)

Suy ra: \(\frac{{HK}}{{AD}} = \frac{{CK}}{{DF}}\)

Mà AD = DF ⇒ HK = KC hay K là trung điểm cạnh HC.

d) Ta có: \(\frac{{CK}}{{AD}} = \frac{{EK}}{{EA}}\) (do CK // AD)

\(\frac{{KH}}{{AD}} = \frac{{BK}}{{BD}}\) (do HK // AD)

Mà CK = HK

⇒ \(\frac{{EK}}{{EA}} = \frac{{BK}}{{BD}}\)

⇒ \(\frac{{EK}}{{EA - EK}} = \frac{{BK}}{{BD - BK}}\)

⇒ \(\frac{{EK}}{{AK}} = \frac{{BK}}{{DK}}\)

⇒ \(\frac{{EK}}{{BK}} = \frac{{AK}}{{DK}}\)

⇒ EB // AD (định lý Ta–lét đảo)

Mà AD ⊥ AB ⇒ BE ⊥ AB

⇒ EB là tiếp tuyến của (O).