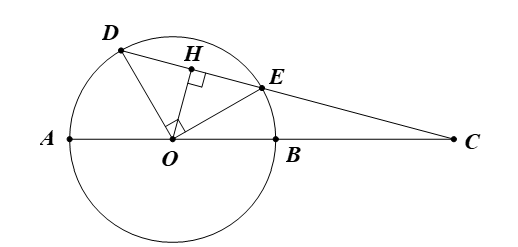
Cho đường tròn (O; R), đường kính AB, dây cung DE. Tia DE cắt AB ở C. Biết $\widehat{DOE}=90°$  và OC = 3R.

a) Tính độ dài CD và CE theo R.

a)

Ta có OD = OE = R và $\widehat{DOE}=90°$  .

Suy ra ∆ODE vuông cân tại O.

Khi đó $DE=\sqrt{O{D}^2+O{E}^2}=\sqrt{R^2+R^2}=R\sqrt{2}$  .

Kẻ OH ⊥ DE tại H.

∆ODE vuông cân tại O có OH là đường cao.

Suy ra OH cũng là đường trung tuyến của ∆ODE.

Do đó H là trung điểm của DE.

Vì vậy $DH=HE=\frac{DE}{2}=\frac{R\sqrt{2}}{2}$  .

∆ODE vuông cân tại O có OH là đường cao: $\frac{1}{O{H}^2}=\frac{1}{O{D}^2}+\frac{1}{O{E}^2}=\frac{1}{R^2}+\frac{1}{R^2}=\frac{2}{R^2}$.

Suy ra $O{H}^2=\frac{R^2}{2}$ .

Khi đó $OH=\frac{R\sqrt{2}}{2}$ .

∆OCH vuông tại H:$CH=\sqrt{O{C}^2-O{H}^2}=\sqrt{9R^2-{\left(\frac{R\sqrt{2}}{2}\right)}^2}=\frac{R\sqrt{34}}{2}$

Ta có $CE=CH-HE=\frac{R\sqrt{34}}{2}-\frac{R\sqrt{2}}{2}=\frac{R\left(\sqrt{34}-\sqrt{2}\right)}{2}$  .

Lại có $CD=CE+DE=\frac{R\left(\sqrt{34}-\sqrt{2}\right)}{2}+R\sqrt{2}=\frac{R\left(\sqrt{34}+\sqrt{2}\right)}{2}$ .