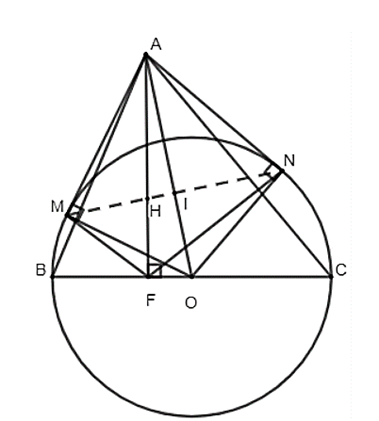
Cho đường tròn (O), đường kính BC = 2R, điểm A nằm ngoài đường tròn sao cho tam giác ABC nhọn. Từ A kẻ 2 tiếp tuyến AM, AN với đường tròn (O). Gọi H là trực tâm của tam giác ABC, F là giao điểm của AH và BC. Chứng minh rằng:
a) 5 điểm A, O, M, N, F cùng nằm trên 1 đường tròn.
b) 3 điểm M, N, H thẳng hàng.
c) HA . HF = R2 – OH2.
a) \(\widehat {AMO} = \widehat {AFO} = \widehat {ANO} = 90^\circ \)
⇒ A, M, F, N, O cùng thuộc một đường tròn
b) Gọi I là giao của MN và AO nên I là trung điểm của MN ⇒ AI.AO = AM2
Xét ∆AMH và ∆AFM có:
\(\widehat {MAH}\)chung
\(\widehat {AMH} = \widehat {AFM}\)
Nên ∆AMH ~ ∆AFM (g.g)
⇒ AH.AF = AM2 = AI.AO
⇒ \(\widehat {AHI} = \widehat {AOF}\)
⇒ OFHI nội tiếp
⇒ M, N, H thẳng hàng
c) Từ câu a) ta có: HM.HN = HA.HF
Ta có: HM.HN = (IM – IH).(IH + IN)
= (IM – IH).(IH + IM)
= IM2 – IH2
= OM2 – OI2 – (OH2 – OI2)
= R2 – OH2
Từ đó suy ra: HA.HF = R2 – OH2.