Cho điểm M bất kì trên đường tròn tâm O đường kính AB. Tiếp tuyến tại M và tại B của (O) cắt nhau tại D. Qua O kẻ đường thẳng vuông góc với OD cắt MD tại C và cắt BD tại N.

a) Chứng minh DC = DN.

b) Chứng minh AC là tiếp tuyến của đường tròn tâm O.

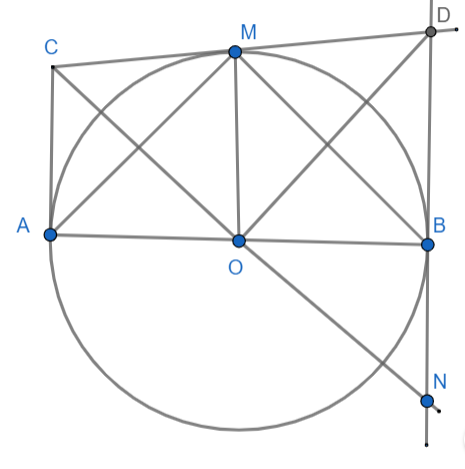
a) Xét đường tròn (O) có MD và BD là tiếp tuyến với B, D là tiếp điểm
⇒ MD = DB (tính chất tiếp tuyến)
Xét tam giác MOD và tam giác BOD có:
MD = BD (cmt)
MO = OB (cùng là bán kính đường tròn)
OD chung
⇒ ΔMOD = ΔBOD 
⇒ $\widehat{MDO}=\widehat{BDO}$ OD là phân giác $\widehat{MDB}$
Xét tam giác CDN có:
OD là đường cao (do OD ⊥ CN)
OD là phân giác $\widehat{MDB}$
Suy ra tam giác CDN cân tại D, suy ra CD = ND (đpcm)
b) Chứng minh AC là tiếp tuyến của đường tròn tâm O.
Xét tam giác CND cân tại D có OD là đường cao ứng với đỉnh D, suy ra OD đồng thời là trung trực ứng với cạnh CN, suy ra CO = ON
Xét tam giác COA và tam giác BON có:
CO = ON (cmt)
OA = OB (do cùng là bán kính)
$\widehat{COA}=\widehat{NOB}$(hai góc đối đỉnh)
⇒ΔCOA = ΔBON ⇒ $\widehat{CAO}=\widehat{NBO}$= 90°
Xét đường tròn tâm O có AC vuông góc với AO, AO là bán kính đường tròn, suy ra AC là tiếp tuyến của đường tròn (đpcm)