Câu hỏi:
01/02/2024 68Cho ∆ABC vuông tại A, M là trung điểm của AC. Kẻ AD và CE vuông góc với BM. Chọn khẳng định đúng:
A. BD + BE > 2AB;
B. BD + BE > 2BM;
C. BD + BE < 2BM;
D. BD + BE < 2AB.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
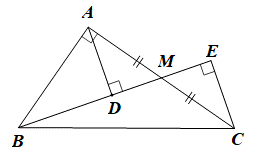
Do AD và CE vuông góc với BM nên \(\widehat {{\rm{ADM}}} = 90^\circ \) và \(\widehat {{\rm{CEM}}} = 90^\circ \).
Xét DADM và DCEM có:
\(\widehat {ADM} = \widehat {CEM}\left( { = 90^\circ } \right),\)
AM = CM (vì M là trung điểm của AC),
\(\widehat {{\rm{AMD}}} = \widehat {{\rm{CME}}}\) (hai góc đối đỉnh).
Suy ra ∆ADM = ∆CEM (cạnh huyền – góc nhọn).
Do đó DM = EM (hai cạnh tương ứng).
Ta có BD + BE = BD + (BM + ME) = (BD + ME) + BM
Mà DM = ME (chứng minh trên)
Nên BD + BE = (BD + DM) + BM = BM + BM = 2BM (1)
Vì BA, BM lần lượt là đường vuông góc và đường xiên kẻ từ B đến AC nên BM > AB.
Hay 2BM > 2AB (2)
Từ (1) và (2) suy ra BD + BE = 2BM > 2AB.
Do đó BD + BE > 2AB
Vậy ta chọn phương án A.
Hướng dẫn giải
Đáp án đúng là: A

Do AD và CE vuông góc với BM nên \(\widehat {{\rm{ADM}}} = 90^\circ \) và \(\widehat {{\rm{CEM}}} = 90^\circ \).
Xét DADM và DCEM có:
\(\widehat {ADM} = \widehat {CEM}\left( { = 90^\circ } \right),\)
AM = CM (vì M là trung điểm của AC),
\(\widehat {{\rm{AMD}}} = \widehat {{\rm{CME}}}\) (hai góc đối đỉnh).
Suy ra ∆ADM = ∆CEM (cạnh huyền – góc nhọn).
Do đó DM = EM (hai cạnh tương ứng).
Ta có BD + BE = BD + (BM + ME) = (BD + ME) + BM
Mà DM = ME (chứng minh trên)
Nên BD + BE = (BD + DM) + BM = BM + BM = 2BM (1)
Vì BA, BM lần lượt là đường vuông góc và đường xiên kẻ từ B đến AC nên BM > AB.
Hay 2BM > 2AB (2)
Từ (1) và (2) suy ra BD + BE = 2BM > 2AB.
Do đó BD + BE > 2AB
Vậy ta chọn phương án A.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác MNP có chu vi bằng 70 cm, biết MN : NP = 2 : 3 và NP : MP = 4 : 5. Trong ba góc của tam giác MNP, góc nào nhỏ nhất?
Câu 2:
Cho tm giác ABC vuông tại C có CH là đường cao. Trên cạnh AB lấy điểm M sao cho BM = BC. Kẻ MN vuông góc với AC tại N. Chọn khẳng định đúng:


