Cho ∆ABC vuông tại A (AB < AC). Kẻ BD là phân giác củagóc ABD (D thuộc AC)
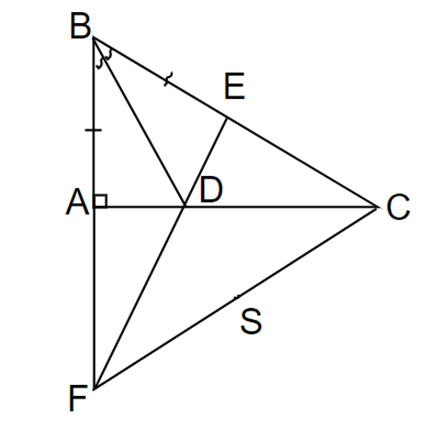
Cho ∆ABC vuông tại A (AB < AC). Kẻ BD là phân giác của \(\widehat {ABD}\) (D thuộc AC), trên cạnh BC lấy điểm E sao cho AB = BE.
a) Chứng minh ∆ABD = ∆EBD.
b) So sánh AD và DC.
c) Đường thẳng ED cắt đường thẳng AB tại F, gọi S là trung điểm của FC. Chứng minh ba điểm B, D, S thẳng hàng.