Biện luận theo m, số nghiệm của phương trình x^3 - 3x^2 - m = 0
Biện luận theo m, số nghiệm của phương trình x3 – 3x2 – m = 0.
Ta có: x3 – 3x2 – m = 0
⇔ m = x3 – 3x2 = f(x)
f’(x) = 3x2 – 6x = 0
⇔ \(\left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\)
Ta có bảng biến thiên:
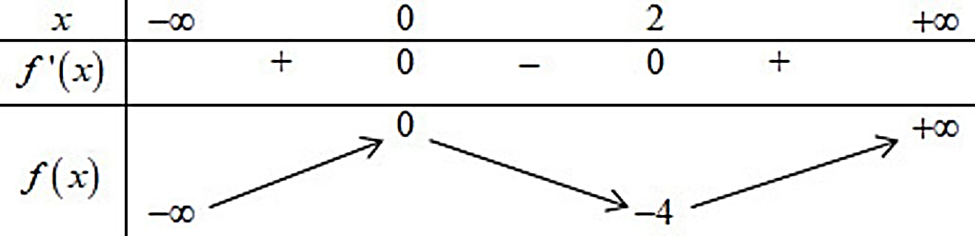
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = m
Dựa vào bảng biến thiên ta thấy:
\(\left[ \begin{array}{l}m < - 4\\m > 0\end{array} \right.\) thì phương trình có nghiệm duy nhất
\(\left[ \begin{array}{l}m = - 4\\m = 0\end{array} \right.\) thì phương trình có 2 nghiệm
– 4 < m < 0 thì phương trình có 3 nghiệm phân biệt.