Bất phương trình mx2 – (2m – 1)x + m + 1 < 0 vô nghiệm khi và chỉ khi: A. m <= 1/8
Bài 6.50 trang 25 SBT Toán 10 Tập 2: Bất phương trình mx2 – (2m – 1)x + m + 1 < 0 vô nghiệm khi và chỉ khi
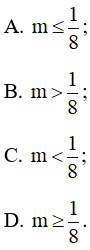
Bài 6.50 trang 25 SBT Toán 10 Tập 2: Bất phương trình mx2 – (2m – 1)x + m + 1 < 0 vô nghiệm khi và chỉ khi
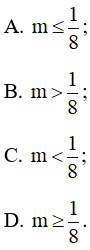
Đáp án đúng là: D
+) Khi m = 0, ta có:
mx2 – (2m – 1)x + m + 1 < 0
⇔ x + 1 < 0
⇔ x < –1
Do đó, m = 0 không thỏa mãn yêu cầu đề bài
+) Khi m ≠ 0, ta có:
Xét tam thức: f(x) = mx2 – (2m – 1)x + m + 1 có:
a = m,
∆ = [–(2m – 1)2] – 4.m.(m + 1) = 4m2 – 4m + 1 – 4m2 – 4m = –8m + 1
Để mx2 – (2m – 1)x + m + 1 < 0 vô nghiệm khi và chỉ khi mx2 – (2m – 1)x + m + 1 ≥ 0 với mọi số thực x
Vậy khi thì bất phương trình mx2 – (2m – 1)x + m + 1 < 0 vô nghiệm.
Xem thêm các bài giải SBT Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
Bài 17: Dấu của tam thức bậc hai
Bài 18: Phương trình quy về phương trình bậc hai
Bài 19: Phương trình đường thẳng
Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách