Với mỗi hàm số dưới đây, hãy vẽ đồ thị, tìm tập giá trị, khoảng đồng biến, khoảng nghịch biến của nó

Bài 6.30 trang 28 Toán 10 Tập 2: Với mỗi hàm số dưới đây, hãy vẽ đồ thị, tìm tập giá trị, khoảng đồng biến, khoảng nghịch biến của nó:

a) y = – x² + 6x – 9; 

b) y = – x² – 4x + 1; 

c) y = x² + 4x; 

d) y = 2x² + 2x + 1. 

Trả lời

a) y = – x² + 6x – 9 là hàm số bậc hai nên đồ thị là một parabol. 

Hệ số a = – 1 < 0 nên bề lõm của đồ thị quay xuống dưới. 

Parabol trên có: 

+ Tọa độ đỉnh I(3; 0);

+ Trục đối xứng x = 3;

+ Cắt trục Oy tại điểm A(0; – 9);

+ Điểm đối xứng với A qua trục đối xứng x = 3 là B(6; – 9);

+ Lấy điểm D(1; – 4) thuộc parabol, điểm đối xứng với D là trục đối xứng x = 3 là E(5; – 4).

Vẽ đường cong đi qua các điểm trên ta được đồ thị hàm số cần vẽ. 

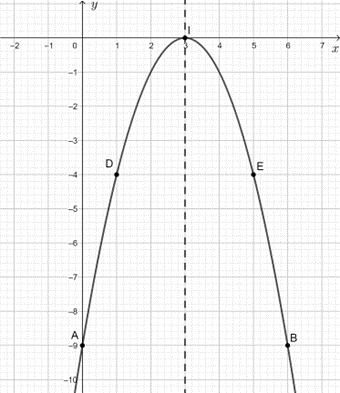
Quan sát đồ thị ta thấy:

+ Tập giá trị của hàm số là (– ∞; 0].

+ Hàm số đồng biến trên khoảng (– ∞; 3) (do đồ thị hàm số đi lên từ trái sang phải) và nghịch biến trên khoảng (3; + ∞) (do đồ thị hàm số đi xuống từ trái sang phải). 

b) y = – x² – 4x + 1 là hàm số bậc hai nên đồ thị là một parabol. 

Hệ số a = – 1 < 0 nên bề lõm của đồ thị quay xuống dưới. 

Parabol trên có: 

+ Tọa độ đỉnh I(– 2; 5);

+ Trục đối xứng x = – 2; 

+ Cắt trục Oy tại điểm A(0; 1);

+ Điểm đối xứng với A qua trục đối xứng x = – 2 là B(– 4; 1);

+ Lấy điểm C(– 1; 4) thuộc đồ thị, điểm đối xứng với C qua trục đối xứng x = – 2 là D(– 3; 4).

Vẽ đường cong đi qua các điểm trên ta được đồ thị hàm số cần vẽ. 

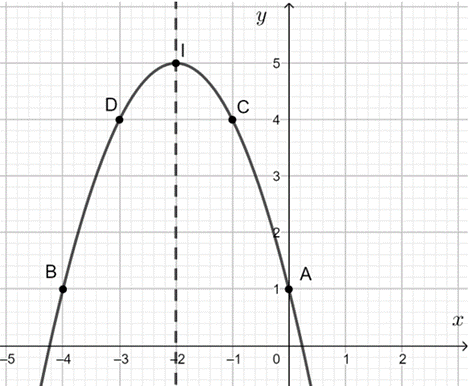
Quan sát đồ thị hàm số ta thấy:

+ Tập giá trị của hàm số là (– ∞; 5]. 

+ Hàm số đồng biến trên khoảng (– ∞; – 2) và nghịch biến trên khoảng (– 2; + ∞). 

c) y = x² + 4x là hàm số bậc hai nên đồ thị là một parabol. 

Hệ số a = 1 > 0 nên bề lõm của đồ thị quay lên trên. 

Parabol trên có: 

+ Tọa độ đỉnh I(– 2; – 4);

+ Trục đối xứng x = – 2;

+ Cắt trục Oy tại điểm gốc tọa độ O(0; 0);

+ Điểm đối xứng với O qua trục đối xứng x = – 2 là điểm B(– 4; 0);

+ Lấy điểm C(– 1; – 3) thuộc đồ thị, điểm đối xứng với C qua trục đối xứng x = – 2 là D(– 3; – 3).

Vẽ đường cong đi qua các điểm trên ta được đồ thị cần vẽ. 

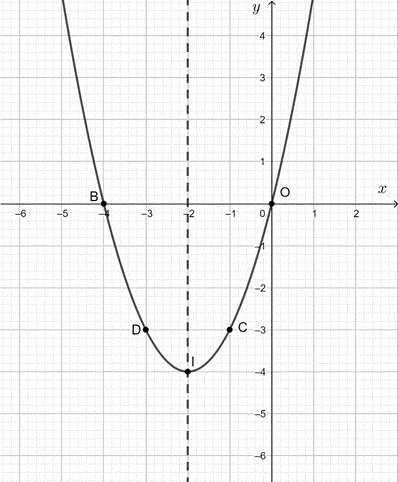
Quan sát đồ thị hàm số ta thấy:

+ Tập giá trị của hàm số là [– 4; + ∞).

+ Hàm số nghịch biến trên khoảng (– ∞; – 2) và đồng biến trên khoảng (– 2; + ∞).

d) y = 2x² + 2x + 1 là hàm số bậc hai nên đồ thị là một parabol. 

Hệ số a = 2 > 0 nên bề lõm của đồ thị quay lên trên. 

Parabol trên có: 

+ Tọa độ đỉnh I$\left(-\frac{1}{2};\frac{1}{2}\right)$;

+ Trục đối xứng x = $-\frac{1}{2}$; 

+ Cắt trục Oy tại điểm A(0; 1).

+ Điểm đối xứng với A qua trục đối xứng x = $-\frac{1}{2}$ là B(– 1; 1);

+ Lấy điểm C(1; 5) thuộc đồ thị, điểm đối xứng với C qua trục đối xứng x =$-\frac{1}{2}$ là D(– 2; 5). 

Vẽ đường cong đi qua các điểm đã cho ta được đồ thị cần vẽ. 

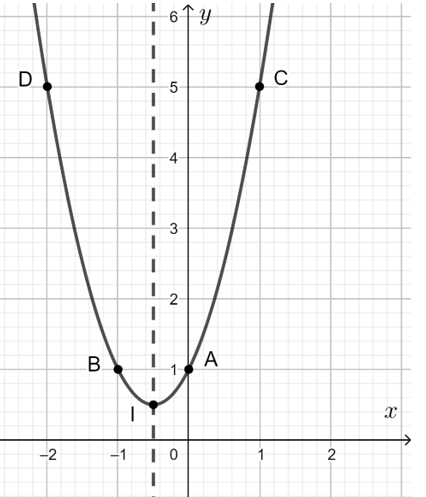
Quan sát đồ thị ta thấy:

+ Tập giá trị của hàm số là $\left[\frac{1}{2};+\infty \right)$.

+ Hàm số nghịch biến trên khoảng $\left(-\infty ;-\frac{1}{2}\right)$ và đồng biến trên khoảng $\left(-\frac{1}{2};+\infty \right)$.