a) Trong Hình 11, cho biết ΔABC ᔕ ΔA′B′C′. Viết tỉ số đồng dạng của các cạnh tương ứng và chỉ ra các cặp góc tương ứng. b) Trong Hình 12, cho biết ΔDEF ᔕ ΔD′E′F′. Tính số đo
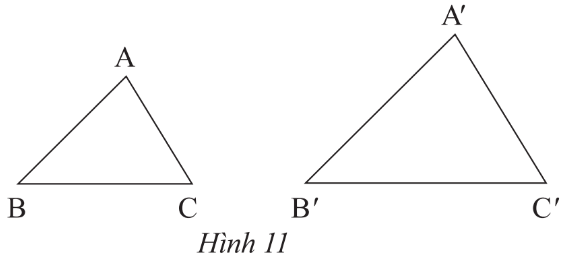
a) Trong Hình 11, cho biết ΔABC ᔕ ΔA′B′C′. Viết tỉ số đồng dạng của các cạnh tương ứng và chỉ ra các cặp góc tương ứng.
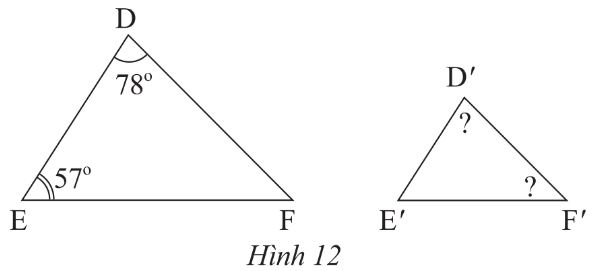
b) Trong Hình 12, cho biết ΔDEF ᔕ ΔD′E′F′. Tính số đo ^D′và ^F′
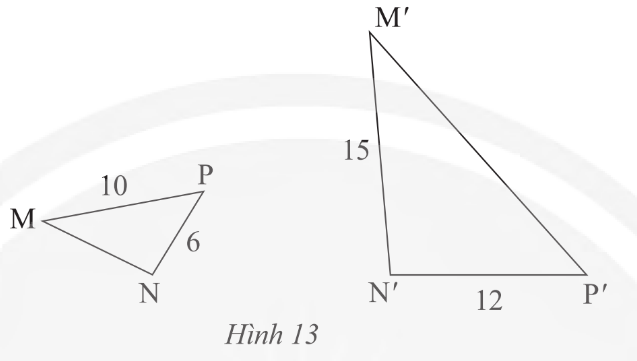
c) Trong Hình 13, cho biết ΔMNP ᔕ ΔM′N′P′. Tính độ dài các đoạn thẳng MN và M'P'.