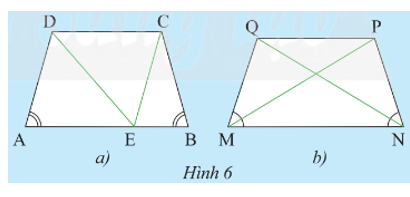
a) Cho hình thang cân ABCD có hai đáy là AB và CD (AB > CD). Qua C vẽ đường thẳng song song với AD và cắt AB tại E (Hình 6a).

   i) Tam giác CEB là tam giác gì? Vì sao?

a)

i) Xét hình thang cân ABCD (AB // DC) có $\widehat{A}=\widehat{B}$.

Vì CE // AD nên $\widehat{A}=\widehat{E}$ (đồng vị).

Do đó $\widehat{E}=\widehat{B}$.

Xét DCEB có $\widehat{E}=\widehat{B}$ nên là tam giác cân tại C.

ii) Do DCEB cân tại C (câu i) nên CE = CB       (1)

Xét DADE và DCED có:

$\widehat{ADE}=\widehat{CED}$ (hai góc so le trong của AD // CE);

DE là cạnh chung;

$\widehat{DEA}=\widehat{EDC}$ (hai góc so le trong của DC // AB).

Do đó DADE = DCED (g.c.g).

Suy ra AD = CE (hai cạnh tương ứng)        (2)

Từ (1) và (2) ta có AD = BC.