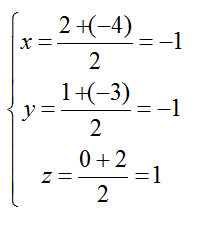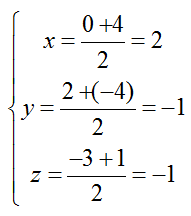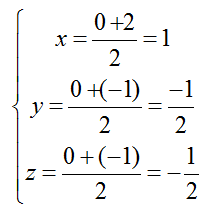Cách viết phương trình mặt phẳng trung trực của đoạn thẳng và bài tập có đáp án (2024)

Viết phương trình mặt phẳng trung trực của đoạn thẳng

Mặt phẳng trung trực là gì ?

Trong không gian cho đoạn thẳng AB và điểm I là trung điểm của AB. Khi đó tồn tại duy nhất một mặt phẳng (P) đi qua I và vuông góc với đoạn thẳng AB. Mặt phẳng (P) được gọi là mặt phẳng trung trực của đoạn thẳng AB.

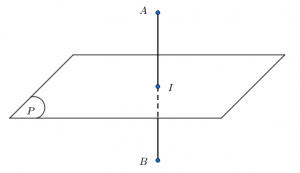
Nếu phát biểu dưới dạng quỹ tích thì mặt phẳng trung trực là quỹ tích các điểm cách đều hai điểm cho trước.

Phương trình mặt phẳng trung trực của đoạn thẳng

1. Phương pháp giải

+ Phương trình mặt phẳng đi qua điểm M (x_o; y_o; z_o) và có vecto pháp tuyến n→(A:B:C) là:

A(x – x_o) + B( y – y_o) + C(z- z_o ) = 0

+ Cho trước hai điểm A và B. Viết phương trình mặt phẳng trung trực của AB :

• Gọi I là trung điểm của AB. Suy ra tọa độ điểm I ( áp dụng công thức trung điểm của đoạn thẳng).

• Mặt phẳng trung trực của AB đi qua điểm I và nhận AB→ làm vecto pháp tuyến

=> Phương trình mặt phẳng trung trực của AB.

2. Ví dụ minh họa

Ví dụ 1: Cho hai điểm A( 2; 1; 0) và B(-4 ; -3; 2) . Viết phương trình mặt phẳng trung trực của AB?

A. 3x + 2y - z+ 6= 0    B. 6x- 4y + 4z+ 3= 0

C. 3x – 2y – 2z+ 4= 0    D. 6x + 4y + 4z+ 1= 0

Hướng dẫn giải:

+ Gọi (P) là mặt phẳng trung trực của AB.

=> Mặt phẳng ( P) nhận AB→ (- 6; -4; 2) làm vecto pháp tuyến. Chọn n→ ( 3; 2; -1)

+ Gọi I là trung điểm của AB; tọa độ điểm I là:

=> I( -1; - 1; 1)

+ Mặt phẳng ( P) qua I (- 1; -1; 1) và vecto pháp tuyến có phương trình là:

3( x+ 1)+ 2( y+ 1) – 1( z – 1) = 0 hay 3x + 2y – z + 6 = 0

Chọn A.

Ví dụ 2: Cho hai điểm A( 0; 2; -3) và B( 4; -4; 1). Gọi M là trung điểm của AB.Viết phương trình mặt phẳng trung trực của OM?

A. 2x + y +z+ 3= 0    B. 2x + y - z+ 3= 0

C. 2x – y – z - 3 = 0    D. 2x – y + z+ 1= 0

Hướng dẫn giải:

+ Do M là trung điểm của AB nên tọa độ của M là:

=> M( 2; -1; -1)

+ Gọi (P) là mặt phẳng trung trực của OM.

=> Mặt phẳng ( P) nhận OM→(2;-1;-1) làm vecto pháp tuyến

+ Gọi I là trung điểm của OM; tọa độ điểm I là:

+ Mặt phẳng ( P) qua I và vecto pháp tuyến OM→(2;-1;-1) có phương trình là:

2.(x-1) - 1.(y+1/2) - 1.(z+1/2) = 0 hay 2x – y – z – 3= 0

Chọn C.

Ví dụ 3: Trong mặt phẳng tọa độ Oxyz; cho hai điểm A và B. Gọi I là trung điểm của AB. Viết phương trình mặt phẳng trung trực của AB biết tọa độ điểm A( 1; 2; 0) và I( -2; 1; 1)

A. x + y- z+ 1= 0    B. 3x+ y- z+ 6= 0

C. 3x- y+ z- 1= 0    D. Tất cả sai

Hướng dẫn giải:

+ Gọi (P) là mặt phẳng trung trực của AB .

=> Mặt phẳng ( P) đi qua I và vuông góc AI

=> Mặt phẳng ( P) đi qua I ( -2; 1; 1) và nhận vecto IA→ ( 3; 1; -1) làm vecto pháp tuyến

Phương trình mặt phẳng (P):

3( x+ 2) + 1( y-1) – 1(z- 1) = 0 hay 3x+ y – z+ 6= 0

Chọn B.

Bài tập vận dụng (có đáp án)

Bài 1: Viết phương trình mặt phẳng trung trực của đoạn thẳng AB biết A(1; -2; 4), B(3; 6; 2).

Lời giải:

Đoạn thẳng AB có trung điểm là I(2; 2; 3).

Mặt phẳng trung trực của đoạn AB đi qua I có vecto pháp tuyến là: 

Phương trình mặt phẳng trung trực của đoạn AB là: 1(x – 2) + 4(y – 2) – 1(z – 3) = 0 hoặc x + 4y – z – 7 = 0

Bài 2: Trong không gian Oxyz, cho điểm A(1;2;3) và điểm B(3;6;1). Biết mặt phẳng (P) là mặt phẳng trung trực của đoạn thẳng AB. Hãy viết phương trình tổng quát của (P).

Lời giải:

Trung điểm I của đoạn thẳng AB có tọa độ là (2;4;2).

Véc tơ AB có tọa độ (2;4;−2) là một véc tơ pháp tuyến của mặt phẳng (P).

Do đó phương trình mặt phẳng (P) là:

2(x−2)+4(y−4)−2(z−2)=0

⇔2x+4y−2z−16=0

⇔x+2y−z−8=0.

Bài 3: Viết phương trình mặt phẳng trung trực của đoạn thẳng AB với A(2; 3; 7), B(4; 1; 3).

Lời giải:

Gọi M là trung điểm của AB.

Tọa độ

M: $\Rightarrow \left\{\begin{array}{c}{x}_M=\frac{x_A+x_B}{2}=3\\ y_M=\frac{y_A+y_B}{2}=2\\ z_M=\frac{z_A+z_B}{2}=5\end{array}\right.\Rightarrow M(3;2;5)$

Do (P) là mặt phẳng trung trực của đoạn thẳng AB nên mp(P) đi qua trung điểm M và nhận vectơ $\overrightarrow{AB}(2;-2;-4)$ làm VTPT

Phương trình mặt phẳng (P) là:

2(x – 3 ) – 2( y – 2) – 4 (z – 5) = 0

Hay 2x – 2y – 4z + 18 = 0

Hay x – y – 2z + 9 = 0.

Bài 5: Tìm phương trình mặt phẳng trung trực của đoạn $AB$ 

Trong không gian $Oxyz$, cho $A(-1;-1;1)$, $B(3;1;1)$. Phương trình mặt phẳng trung trực của đoạn $AB$ là.

Lời giải

Gọi $I$ là trung điểm của $AB$ nên $I(1;0;1)$.

Mặt phẳng trung trực của đoạn $AB$có vtpt là $\overrightarrow{n}$$=\overrightarrow{AB}$$=(4;2;0)$$=2(2;1;0)$.

Phương trình mặt phẳng cần tìm là: $2(x-1)+1(y-0)=0$$\iff 2x+y-2=0$.

Bài 6: Tìm Phương trình mặt phẳng trung trực đoạn $AB$

Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $A(1;6;-7)$ và $B(3;2;1)$. Phương trình mặt phẳng trung trực đoạn $AB$ là.

Lời giải

Mặt phẳng trung trực đoạn $AB$ đi qua trung điểm $I(2;4;-3)$ của đoạn $AB$ và nhân $\overrightarrow{AB}=(2;-4;8)$ làm vectơ pháp tuyến có phương trình:

$2(x-2)-4(y-4)+8(z+3)=0$$\iff x-2y+4z+18=0$

Bài 7: Viết phương trình mặt phẳng trung trực $\left(\alpha \right)$ của đoạn thẳng$AB$

Trong không gian $Oxyz$, cho hai điểm $A(1;3;-4)$ và $B(-1;2;2)$. Viết phương trình mặt phẳng trung trực $\left(\alpha \right)$ của đoạn thẳng$AB$.

A. $\left(\alpha \right):4x+2y+12z+7=0$.                                 B. $\left(\alpha \right):4x-2y+12z+17=0$.

C. $\left(\alpha \right):4x+2y-12z-17=0$.                                 D. $\left(\alpha \right):4x-2y-12z-7=0$.

Lời giải

Gọi $I(0;\frac{5}{2};-1)$ là trung điểm của $AB$; $\overrightarrow{AB}=(-2;-1;6)$.

Mặt phẳng $\left(\alpha \right)$ qua $I(0;\frac{5}{2};-1)$ và có VTPT $\overrightarrow{n}=(-2;-1;6)$ nên có PT:$\left(\alpha \right):-2\left(x\right)-(y-\frac{5}{2})+6(z+1)=0\iff 4x+2y-12z-17=0$.

Do đó, đáp án chính xác của bài này chính là C.

Bài 8: Viết phương trình mặt phẳng trung trực của đoạn thẳng $AB$

Trong không gian $Oxyz$, cho hai điểm $A(1;-1;2)$ và $B(3;3;0)$. Mặt phẳng trung trực của đoạn thẳng $AB$ có phương trình là

A. $x+y-z-2=0$.                 B. $x+y-z+2=0$.           

C. $x+2y-z-3=0$.              D. $x+2y-z+3=0$.

Lời giải

Ta có $\overrightarrow{AB}=2(1;2;-1)$.

Gọi $I$ là trung điểm của $AB\Rightarrow I(2;1;1)$.

+ Mặt phẳng trung trực$\left(\alpha \right)$ của đoạn thẳng $AB$ đi qua $I$và nhận $\overrightarrow{n}=\frac{1}{2}\overrightarrow{AB}=(1;2;-1)$ làm vectơ pháp tuyến có phương trình là

$x-2+2(y-1)-(z-1)=0\iff x+2y-z-3=0$.

Vậy mặt phẳng trung trực của đoạn thẳng $AB$ là $x+2y-z-3=0$.

Do đó, đáp án chính xác của bài này chính là C.

Bài 9: Khẳng định nào sau đây là đúng

Trong không gian với hệ tọa độ$Oxyz$, cho điểm $A(2;4;1);B(-1;1;3)$ và mặt phẳng $\left(P\right):x-3y+2z-5=0$. Một mặt phẳng $\left(Q\right)$ đi qua hai điểm $A,B$ và vuông góc với mặt phẳng $\left(P\right)$ có dạng $ax+by+cz-11=0$. Khẳng định nào sau đây là đúng?

A. $a+b+c=5$.            B. $a+b+c=15$.               C. $a+b+c=-5$.              D. $a+b+c=-15$.

Lời giải

Vì $\left(Q\right)$ vuông góc với $\left(P\right)$ nên $\left(Q\right)$ nhận vtpt $\overrightarrow{n}=(1;-3;2)$của $\left(P\right)$làm vtcp

Mặt khác $\left(Q\right)$đi qua $A$ và $B$ nên $\left(Q\right)$nhận $\overrightarrow{AB}=(-3;-3;2)$ làm vtcp

$\left(Q\right)$ nhận $\overrightarrow{n_Q}=[\overrightarrow{n},\overrightarrow{AB}]=(0;8;12)$ làm vtpt

Vậy phương trình mặt phẳng $\left(Q\right):0(x+1)+8(y-1)+12(z-3)=0$, hay $\left(Q\right):2y+3z-11=0$

Vậy $a+b+c=5$. Do đó, đáp án chính xác của bài này chính là A.

Bài 10: Tìm phương trình Mặt phẳng $\left(Q\right)$

Trong không gian với hệ tọa độ $Oxyz$, cho $A(1;-1;2);B(2;1;1)$ và mặt phẳng $\left(P\right):x+y+z+1=0$. Mặt phẳng $\left(Q\right)$ chứa $A,B$ và vuông góc với mặt phẳng $\left(P\right)$. Mặt phẳng $\left(Q\right)$ có phương trình là:

A. $3x-2y-z-3=0$.                B. $x+y+z-2=0$.                

C. $-x+y=0$.                D. $3x-2y-z+3=0$.

Lời giải

Ta có $\overrightarrow{AB}=(1;2;-1)$

Từ $\left(P\right)$ suy ra vec tơ pháp tuyến của $\left(P\right)$ là $\overrightarrow{n_P}=(1;1;1)$

Gọi vec tơ pháp tuyến của $\left(Q\right)$ là $\overrightarrow{n_Q}$

Vì $\left(Q\right)$ chứa $A,B$ nên $\overrightarrow{n_Q}\mathrm{\perp }\overrightarrow{AB}\left(1\right)$

Mặt khác $\left(Q\right)\mathrm{\perp }\left(P\right)$ nên $\overrightarrow{n_Q}\mathrm{\perp }\overrightarrow{n_P}\left(2\right)$

Từ $\left(1\right),\left(2\right)$ ta được $\overrightarrow{n_Q}=[\overrightarrow{AB},\overrightarrow{n_P}]=(3;-2;-1)$

$\left(Q\right)$ đi qua $A(1;-1;2)$ và có vec tơ pháp tuyến $\overrightarrow{n_Q}=(3;-2;-1)$ nên $\left(Q\right)$ có phương trình là

$3(x-1)-2(y+1)-(z-2)=0$ $\iff 3x-2y-z-3=0$.

Vậy $a+b+c=5$. Do đó, đáp án chính xác của bài này chính là A.

Bài 11: Tìm phương trình mặt phẳng $\left(Q\right)$

Trong không gian với hệ tọa độ $Oxyz$, cho mặt phẳng $\left(P\right):x+y+z+1=0$ và hai điểm $A(1;-1;2);B(2;1;1)$. Mặt phẳng $\left(Q\right)$ chứa $A,B$ và vuông góc với mặt phẳng $\left(P\right)$, mặt phẳng $\left(Q\right)$có phương trình là:

A. $3x-2y-z+3=0$.                B. $x+y+z-2=0$.                

C. $3x-2y-z-3=0$.                D. $-x+y=0$.

Lời giải

Mặt phẳng $\left(P\right)$ có 1 véc tơ pháp tuyến là $\overrightarrow{n_p}=(1;1;1)$. Véc tơ $\overrightarrow{AB}=(1;2;-1)$.

Gọi $\overrightarrow{n}$ là một véc tơ pháp tuyến của $\left(Q\right)$, do $\left(Q\right)$vuông góc với $\left(P\right)$ nên $\overrightarrow{n}$có giá vuông góc với $\overrightarrow{n_p}$, mặt khác véc tơ $\overrightarrow{AB}$ có giá nằm trong mặt phẳng $\left(Q\right)$ nên $\overrightarrow{n}$ cũng vuông góc với $\overrightarrow{AB}$

Mà ${\overrightarrow{n}}_p$ và $\overrightarrow{AB}$ không cùng phương nên ta có thể chọn $\overrightarrow{n}$=$[\overrightarrow{n_P},\overrightarrow{AB}]=(-3;2;1)$, mặt khác $\left(Q\right)$đi qua $A(1;-1;2)$ nên phương trình của mặt phẳng $\left(Q\right)$ là:

$-3(x-1)+2(y+1)+1(z-2)=0\iff 3x-2y-z-3=0$.

Do đó, đáp án chính xác ta chọn cho bài này chính là A.

Bài 12: Viết phương trình mặt phẳng $\left(R\right)$ chứa $A$, vuông góc với cả hai mặt phẳng $\left(P\right)$ và $\left(Q\right)$

Trong không gian với hệ tọa độ $Oxyz$, cho điểm $A(1;1;1)$ và hai mặt phẳng $\left(P\right):2x-y+3z-1=0$, $\left(Q\right):y=0$. Viết phương trình mặt phẳng $\left(R\right)$ chứa $A$, vuông góc với cả hai mặt phẳng $\left(P\right)$ và $\left(Q\right)$.

A. $3x-y+2z-4=0$.                B. $3x+y-2z-2=0$.                

C. $3x-2z=0$.                           D. $3x-2z-1=0$.

Lời giải

$\left(P\right):2x-y+3z-1=0$ có véctơ pháp tuyến ${\overrightarrow{n}}_{\left(P\right)}=(2;-1;3)$.

$\left(Q\right):y=0$ có véctơ pháp tuyến ${\overrightarrow{n}}_{\left(Q\right)}=(0;1;0)$.

Do mặt phẳng $\left(R\right)$ vuông góc với cả hai mặt phẳng $\left(P\right)$ và $\left(Q\right)$ nên có véctơ pháp tuyến ${\overrightarrow{n}}_{\left(R\right)}=[{\overrightarrow{n}}_{\left(P\right)},{\overrightarrow{n}}_{\left(Q\right)}]$. $\Rightarrow {\overrightarrow{n}}_{\left(R\right)}=(-3;0;2)$.

Vậy phương trình mặt phẳng $\left(R\right)$ là: $-3x+2z+1=0$$\iff 3x-2z-1=0$.

Do đó, đáp án chính xác ta chọn cho bài này chính là D.

Xem thêm các dạng bài tập liên quan khác:

60 Bài tập về phương trình đường thẳng trong không gian (có đáp án năm 2023)

60 Bài tập về phương trình mặt phẳng (có đáp án năm 2023)

60 Bài tập khái niệm về mặt tròn xoay (có đáp án năm 2023)

60 Bài tập về mặt cầu (có đáp án năm 2023)

60 Bài tập về thể tích khối đa diện ( có đáp án năm 2023 )