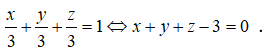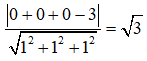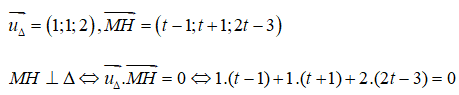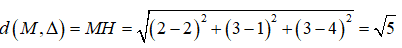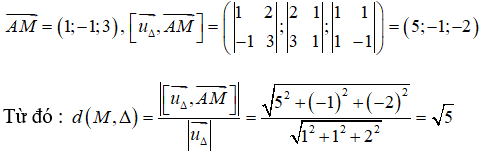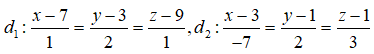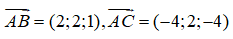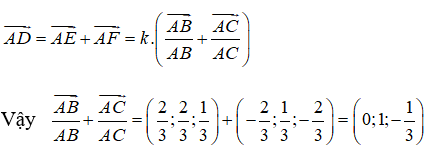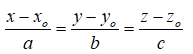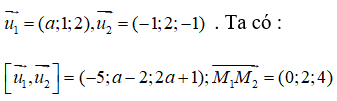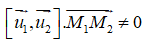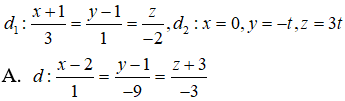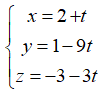60 Bài tập về phương trình đường thẳng trong không gian (có đáp án năm 2024) - Toán 12

Phương trình đường thẳng trong không gian

Kiến thức cần nhớ

I. Phương trình tham số của đường thẳng

-  Định lí:

Trong không gian Oxyz, cho đường thẳng ∆ đi qua điểm M₀ (x₀ ; y₀; z₀) và nhận vectơ $\overrightarrow{a}=\left(a_1;a_2;a_3\right)$ làm vectơ chỉ phương. Điều kiện cần và đủ để điểm M(x; y; z) nằm trên đường thẳng ∆ là có số thực t thỏa mãn: $\left\{\begin{array}{l}x=x_0+a_{1}t\\ y=y_0+a_{2}t\\ z=z_0+a_{2}t\end{array}\right.$

- Định nghĩa:

Phương trình tham số của đường thẳng ∆ đi qua điểm M₀ (x₀ ; y₀; z₀) và nhận vectơ $\overrightarrow{a}=\left(a_1;a_2;a_3\right)$ làm vectơ chỉ phương là $\left\{\begin{array}{l}x=x_0+a_{1}t\\ y=y_0+a_{2}t\\ z=z_0+a_{2}t\end{array}\right.$

Trong đó, t là tham số.

- Chú ý:

Nếu a₁ ; a₂; a₃ đều khác 0 thì ta có thể viết phương trình ∆ dưới dạng chính tắc như sau:

$\frac{x-x_0}{a_1}=\frac{y-y_0}{a_2}$$=\frac{z-z_0}{a_3}$

Ví dụ 1. Viết phương trình tham số của đường thẳng ∆ đi qua A(1; 2;2) và có vecto chỉ phương là $\overrightarrow{u}(1;2;-1)$

Lời giải:

Phương trình tham số của ∆ là: $\left\{\begin{array}{c}x=1+\text{}t\\ y=2+\text{}2t\\ z=2-t\end{array}\right.$

Ví dụ 2. Viết phương trình tham số của đường thẳng AB với A(0;1; 2); B(2; 2; 1).

Lời giải:

Đường thẳng AB nhận $\overrightarrow{AB}(2;1;-1)$ làm vecto chỉ phương.

Phương trình tham số của AB là: $\left\{\begin{array}{c}x=2\text{}t\\ y=1+\text{}t\\ z=2-t\end{array}\right.$.

II. Điều kiện để hai đường thẳng song song, cắt nhau và chéo nhau.

1. Điều kiện để hai đường thẳng song song.

 Gọi $\overrightarrow{a}=(a_1;a_2;a_3);$$\overrightarrow{a\text{'}}=(a{\text{'}}_1;a{\text{'}}_2;a{\text{'}}_3)$ lần lượt là vecto chỉ phương của d và d’.

Lấy điểm M(x₀; y₀; z₀) trên d.

Ta có: d song song với d’ khi và chỉ khi $\left\{\begin{array}{c}\overrightarrow{a}=k.\overrightarrow{a\text{'}}\\ M\notin d\text{'}\end{array}\right.$

Đặc biệt: d trùng với d’ khi và chỉ khi: $\left\{\begin{array}{c}\overrightarrow{a}=k.\overrightarrow{a\text{'}}\\ M\in d\text{'}\end{array}\right.$

Ví dụ 3.  Chứng minh hai đường thẳng sau đây song song với nhau:

$d:\left\{\begin{array}{c}x=3+\text{}2t\\ y=2-3t\\ z=2+t\end{array}\right.$;$\hspace{0.17em}\hspace{0.17em}d\text{'}:\left\{\begin{array}{c}x=1-\text{}4t\\ y=2+\text{}6t\\ z=-2t\end{array}\right.$

Lời giải:

Đường thẳng d có vecto chỉ phương $\overrightarrow{u}(2;-3;1)$ đi qua M(3; 2; 2).

Đường thẳng d’ có vecto chỉ phương là $\overrightarrow{v}(-4;6;-2)$

Ta thấy: $\overrightarrow{v}=-2\overrightarrow{u};M\notin d\text{'}$

Do đó, hai đường thẳng trên song song với nhau.

2. Điều kiện để hai đường thẳng cắt nhau.

- Hai đường thẳng d và d’ cắt nhau khi và chỉ khi hệ phương trình ẩn t và t’ sau:

$\left\{\begin{array}{c}{x}_0+\text{\hspace{0.17em}}t{a}_1=x{\text{'}}_0+\text{\hspace{0.17em}}t\text{'}.a{\text{'}}_1\\ y_0+\text{\hspace{0.17em}}t{a}_2=y{\text{'}}_0+\text{\hspace{0.17em}}t\text{'}.a{\text{'}}_2\\ z_0+\text{\hspace{0.17em}}t{a}_3=z{\text{'}}_0+\text{\hspace{0.17em}}t\text{'}.a{\text{'}}_3\end{array}\right.$ (I)

Có đúng một nghiệm.

- Chú ý: Giả sử hệ (I) có nghiệm (t₀ ; t’₀), để tìm giao điểm M₀ của d và d’ ta có thể thay t₀ vào phương trình tham số của d hoặc thay t’₀ vào phương trình tham số của d’.

Ví dụ 4. Tìm giao điểm của hai đường thẳng:

$d:\left\{\begin{array}{c}x=3+\text{}t\\ y=2-t\\ z=2+t\end{array}\right.$;$d\text{'}:\left\{\begin{array}{c}x=3-\text{}t\text{'}\\ y=2+t\text{'}\\ z=3\end{array}\right.$

Lời giải:

Xét hệ phương trình:

$$\begin{gathered} \left\{\begin{array}{c}3+t=3-t\text{'}\\ 2-t=2+\text{\hspace{0.17em}}t\text{'}\\ 2+\text{}t=3\end{array}\right. \\ \iff \left\{\begin{array}{c}t=-t\text{'}\\ t=-t\text{'}\\ t=1\end{array}\right. \\ \iff t=1;t\text{'}=-1 \end{gathered}$$

Suy ra, d cắt d’ tại điểm A(4; 1; 3).

3. Điều kiện để hai đường thẳng chéo nhau.

Hai đường thẳng d và d’ chéo nhau khi và chỉ khi $\overrightarrow{a};\overrightarrow{a\text{'}}$ không cùng phương và hệ phương trình $\left\{\begin{array}{c}{x}_0+\text{\hspace{0.17em}}t{a}_1=x{\text{'}}_0+\text{\hspace{0.17em}}t\text{'}.a{\text{'}}_1\\ y_0+\text{\hspace{0.17em}}t{a}_2=y{\text{'}}_0+\text{\hspace{0.17em}}t\text{'}.a{\text{'}}_2\\ z_0+\text{\hspace{0.17em}}t{a}_3=z{\text{'}}_0+\text{\hspace{0.17em}}t\text{'}.a{\text{'}}_3\end{array}\right.$ vô nghiệm.

Ví dụ 5. Xét vị trí tương đối của hai đường thẳng:

$d:\left\{\begin{array}{c}x=3+\text{}t\\ y=2-3t\\ z=2+t\end{array};\right.$$\hspace{0.17em}d\text{'}:\left\{\begin{array}{c}x=1-\text{}4t\text{'}\\ y=2+\text{}6t\text{'}\\ z=-2t\text{'}\end{array}\right.$

Lời giải:

Đường thẳng d có vecto chỉ phương $\overrightarrow{a}(1;-3;1)$

Đường thẳng d’ có vecto chỉ phương là $\overrightarrow{a\text{'}}(-4;6;-2)$

Ta thấy, không tồn tại số thực k để $\overrightarrow{a}=k\overrightarrow{a\text{'}}$ nên hai đường thẳng d và d’ cắt nhau hoặc chéo nhau.

Xét hệ phương trình:

$\left\{\begin{array}{c}3+\text{\hspace{0.17em}}t=1-4t\text{'}\left(1\right)\\ 2-3t=2+6t\text{'}\left(2\right)\\ 2+t=-2t\text{'}\left(3\right)\end{array}\right.$ (I)

Giải hệ phương trình (1) và (2) ta được:  t =2; t’ = -1.

Thay vào (3) ta thấy không thỏa mãn nên hệ phương trình (I) vô nghiệm.

Vậy hai đường thẳng d và d’ chéo nhau.

- Nhận xét:

Trong không gian Oxyz, cho mặt phẳng (P): Ax + By + Cz + D = 0 và đường thẳng d: $\left\{\begin{array}{l}x=x_0+a_{1}t\\ y=y_0+a_{2}t\\ z=z_0+a_{2}t\end{array}\right.$

Xét phương trình A(x₀ + ta₁ ) + B(y₀ + ta₂ ) + C (z₀ + ta₃ ) + D = 0 ( t là ẩn ) (1)

- Nếu phương trình (1) vô nghiệm thì d và (P) không có điểm chung. Vậy d// (P).

- Nếu phương trình (1) có đúng một nghiệm t = t₀ thì d cắt (P) tại điểm M(x₀ + t₀ a₁;y₀ + t₀ a₂; z₀ + t₀ a₃).

- Nếu phương trình (1) có vô số nghiệm thì d thuộc (P).

Ví dụ 6. Xét vị trí tương đối của đường thẳng $d:\left\{\begin{array}{c}x=1+\text{}2t\\ \begin{array}{l}y=-t\\ z=-2+t\end{array}\end{array}\right.$

và mặt phẳng (P): 2x – y – z = 0.

Lời giải:
Lấy điểm M(1+ 2t;  -t; -2 + t) thuộc đường thẳng d.

Thay tọa độ điểm M vào phương trình (P) ta được:

2(1+ 2t) – (- t) – (-2+ t) = 0

$\iff$2 + 4t + t + 2 – t  = 0

$\iff$4t + 4 = 0$\iff$t = - 1.

Suy ra đường thẳng d cắt mặt phẳng (P) tại M( -1; 1; - 3).

Các dạng bài tập về phương trình đường thẳng trong không gian

Dạng 1: Viết phương trình tham số và phương trình chính tắc của đường thẳng d biết d đi qua điểm M (x0; y0; z0) và có vectơ chỉ phương u = (a; b; c).

Dạng 2: Viết phương trình tham số của đường thẳng d biết d đi qua hai điểm A, B cho trước.

Dạng 3: Viết phương trình đường thẳng d đi qua điểm M và vuông góc với mặt phẳng (α).

Dạng 4: Viết phương trình đường thẳng d đi qua điểm M và song song với đường thẳng d’.

Dạng 5: Đường thẳng d đi qua điểm M và song song với 2 mặt phẳng cắt nhau (P) và (Q).

Dạng 6: Viết phương trình đường thẳng d đi qua điểm M, song song với mặt phẳng (P) và vuông góc với đường thẳng d’ (d’ không vuông góc với (P)).

Dạng 7 : Viết phương trình đường thẳng d đi qua điểm M và vuông góc với hai đường thẳng d1 và d2 (d1 và d2 là hai đường thẳng chéo nhau).

Dạng 8: Viết phương trình đường thẳng d đi qua điểm M đồng thời cắt cả hai đường thẳng d1 và d2.

Dạng 9: Viết phương trình đường thẳng d đi qua điểm A, vuông góc với đường thẳng d1 và cắt đường thẳng d2.

Dạng 10: Viết phương trình đường thẳng d đi qua điểm A, vuông góc với đường thẳng d1 và cắt đường thẳng d1.

Dạng 11: Viết phương trình đường thẳng d nằm trong mp(P) đồng thời cắt cả hai đường thẳng d1 và d2.

Dạng 12: Viết phương trình đường thẳng d song song với d’ đồng thời cắt cả hai đường thẳng d1 và d2.

Dạng 13: Viết phương trình đường thẳng d song song và cách đều hai đường thẳng song song d1 và d2 đồng thời d nằm trong mặt phẳng chứa d1 và d2.

Dạng 14: Viết phương trình đường thẳng d là đường vuông góc chung của hai đường thẳng d1 và d2 chéo nhau.

Dạng 15 : Viết phương trình tham số của đường thẳng d là hình chiếu của d’ trên mặt phẳng (P).

Bài tập tự luyện

1 Bài tập vận dụng

Câu 1: Trong không gian Oxyz, cho ba điểm A(3;0;0), B(0;3;0), C(0;0;3). Trong những khẳng định dưới đây, khẳng định nào sai?

- Phương trình của mặt phẳng (ABC) là: x + y + z - 3 = 0

- Hình chóp O.ABC là hình chóp tam giác đều

- Phương trình đường thẳng qua O, vuông góc với mặt phẳng (ABC) là: x = t, y = t, z = t

- Khoảng cách từ O đến mặt phẳng ABC bằng 3

Lời giải:

Phương trình mặt phẳng (ABC) là:

Câu 2: Trong không gian Oxyz, cho đường thẳng Δ: x = 1 + 2, y = 2 + t, z = 1 + 2t và điểm M(2; 1; 4). Khoảng cách từ M đến đường thẳng Δ là?

Lời giải:

Cách 1. Gọi H là hình chiếu vuông góc của M trên đường thẳng Δ.

Ta có: H ∈ Δ => H(1 + t; 2 + t; 1 + 2t)

<=> 6t - 6 = 0 <=> t = 1 => H(2; 3; 3)

Vậy khoảng cách từ M đến đường thẳng Δ là:

Vậy đáp án đúng là C

Cách 2. Δ đi qua điểm A(1 ;2 ;1) và có vectơ chỉ phương là

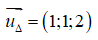
Ta có:

Câu 3: Trong không gian Oxyz, cho hai đường thẳng chéo nhau :

Cho mặt cầu (S) có một đường kính là đoạn vuông góc chung của hai đường thẳng đã cho. Bán kính của mặt cầu (S) là?

Lời giải:

Ta có d₁ đi qua điểm M₁(7; 3; 9) và có vectơ chỉ phương là $\overrightarrow{u_1}$ = (1; 2; 1); d₂ đi qua điểm M₂(3; 1; 1) và có vectơ chỉ phương là $\overrightarrow{u_2}$ .

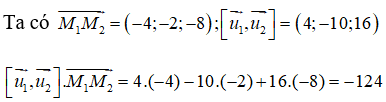
Bán kính của mặt cầu (S) là :

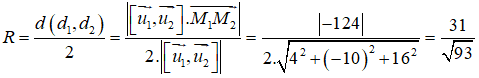
Câu 4: Cho tam giác ABC có ABC có A(2; 2; 1), B(4; 4; 2), C(-2; 4; -3) . Vectơ nào dưới đây là vectơ chỉ phương của đường phân giác trong AD của tam giác ABC.

Lời giải:

Câu 5: Trong không gian Oxyz, cho d là đường thẳng đi qua điểm M₀(x₀; y₀; z₀) và có vectơ chỉ phương là $\overrightarrow{u}$ , với a, b, c khác 0. Trong các khẳng định sau, khẳng định nào sai?

- Phương trình chính tắc của đường thẳng d là:

- Phương trình tham số của đường thẳng d là: x = x₀ + at, y = y₀ + bt, z = z₀ + at

- Đường thẳng d nằm trong hai mặt phẳng :(P): b(x - x₀) - a(y - y₀) = 0 và (Q): c(x - x₀) - a(z - z₀) = 0

- Phương trình đường thẳng d là: a(x - x₀) + b (y - y₀) + c(z - z₀) = 0

Lời giải:

Câu 6: Tìm tất cả các giá trị của a để hai đường thẳng sau chéo nhau :

d₁: x = 1 + at, y = t, z = -1 + 2t, d₂: x = 1 - t', y = 2 + 2t', z = 3 - t'

Lời giải:

Hai đường thẳng d₁, d₂ lần lượt đi qua hai điểm M₁(1; 0; -1), M₂(1; 2; 3) và có vectơ chỉ phương lần lượt là

Hai đường thẳng chéo nhau khi và chỉ khi :

⇔ -5.0 + (a - 2).2 + (2a + 1).4 ≠ 0 ⇔ 10a ≠ 0 ⇔ a ≠ 0

Câu 7: Tìm tất cả các giá trị của a để hai đường thẳng sau vuông góc 

d₁: x = 1 - t, y = 1 + 2t, z = 3 + at, d₂: x = a + at, y = -1 + t, z = -2 + 2t

Lời giải:

Hai đường thẳng đã cho có hai vecto chỉ phương là $\overrightarrow{u_1}$(-1; 2; a); $\overrightarrow{u_2}$(a; 1; 2)

Để hai đường thẳng sau vuông góc thì

$\overrightarrow{u_1}.\overrightarrow{u_2}$ = -1.a + 2.1 + a.2 = 0 ⇔ a + 2 = 0 ⇔ a = -2

Câu 8: Vị trí tương đối của đường thẳng d: x = 1 + 2t, y = 1 - t, z = 1 - t và mặt phẳng (P): x + y + z - 3 = 0 là?

Lời giải:

Đường thẳng d đi qua điểm A( 1 ; 1 ;1) ; có một vecto chỉ phương là ( 2 ; -1 ; -1)

Mặt phẳng (P) có vecto pháp tuyến là

Ta có: $\overrightarrow{u}.\overrightarrow{n}$ = 2.1 + (-1).1 + (-1).1 = 0 và A ∈ (P)

Suy ra, đường thẳng d thuộc mặt phẳng (P).

Câu 9: Vị trí tương đối của đường thẳng d: x = 2 + 4t, y = 3 + t, z = -5t và mặt phẳng (P): x + y + z - 3 = 0 là?

Lời giải:

Đường thẳng d đi qua điểm M(2 ;3 ;0) và có vectơ chỉ phương là $\overrightarrow{ud}$ = (4; 1; -5), mặt phẳng (P) có vectơ pháp tuyến là $\overrightarrow{uP}$ = (1; 1; 1). Ta có :

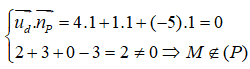
Suy ra đường thẳng d song song với mặt phẳng (P).

Câu 10: Trong không gian Oxyz, lập phương trình tham số của đường thẳng d đi qua điểm M(2;1;-3) và vuông góc với hai đường thẳng:

Lời giải:

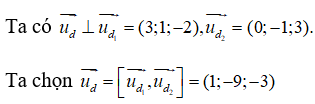
Mặt khác d đi qua điểm M(2 ;1 ;-3).

Vậy phương trình tham số của đường thẳng d là:

x = 2 + t, y = 1 - 9t, z = -3 - 3t

2 Bài tập tự luyện có hướng dẫn

Xem thêm các dạng bài tập Toán chi tiết và hay khác:

80 Bài tập Tổng và hiệu của hai vectơ (có đáp án năm 2023)

80 Bài tập về Tích vô hướng của một vectơ với một số (có đáp án năm 2023)

80 Bài tập về vectơ trong mặt phẳng tọa độ (có đáp án năm 2023)

90 Bài tập tích vô hướng của hai vectơ (có đáp án năm 2023)

90 Bài tập về vị trí tương đối giữa hai đường thẳng, góc và khoảng cách (có đáp án năm 2023)