Cách tính chu vi và diện tích hình thang
I. Phương pháp giải
1.. Hình thang là gì
Khái niệm: Hình thang là một tứ giác lồi có hai cạnh đáy song song, 2 cạnh còn lại được gọi là hai cạnh bên.
Hình thang vuông là hình thang có một góc vuông. Cạnh bên vuông góc với hai đáy cũng chính là chiều cao của hình thang.
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau. 2 cạnh bên của hình thang cân bằng nhau và không song song với nhau.
2. Công thức tính diện tích hình thang
Trước tiên tính công thức chung của hình thang chúng ta sẽ có công thức: trung bình cộng 2 cạnh đáy nhân với chiều cao giữa 2 đáy.
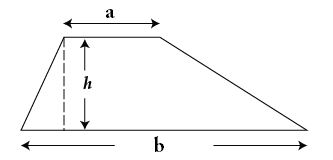
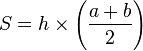
Theo như công thức trên diện tích hình thang định nghĩa bằng lời là Diện tích của hình thang bằng chiều cao nhân với trung bình cộng của tổng hai cạnh đáy.
Còn có bài thơ về tính diện tích hình thang khá dễ nhớ như sau:
Muốn tính diện tích hình thang
Đáy lớn đáy nhỏ ta đem cộng vào
Cộng vào nhân với chiều cao
Chia đôi lấy nửa thế nào cũng ra
Cách tính diện tích hình thang cân
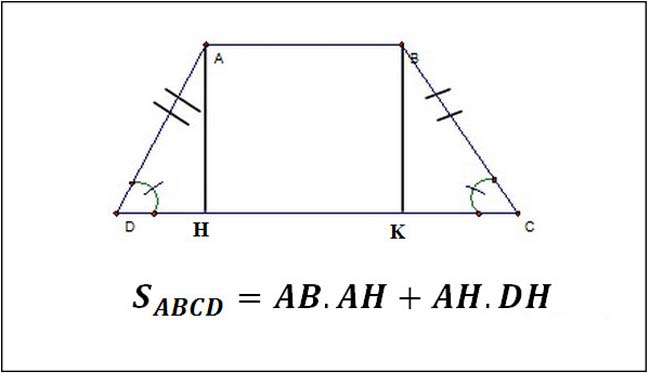
Ngoài việc áp dụng công thức như tính hình thang bình thường, bạn cũng có thể chia nhỏ hình thang cân ra để tính diện tích từng phần rồi cộng lại với nhau.
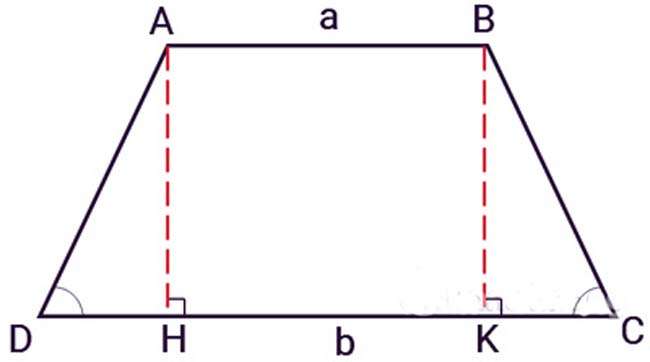
Giả dụ, hình thang cân ABCD có 2 cạnh bên AD và BC bằng nhau. Đường cao AH và BK, hình thang sẽ được chia ra thành 1 hình chữ nhật ABKH và 2 hình tam giác là ADH và BCK. Áp dụng công thức tính diện tích hình chữ nhật cho ABHK và diện tích tam giác cho ADH và BCK sau đó cộng tất cả diện tích để tìm diện tích hình thang ABCD.
3. Công thức tính chu vi hình thang, cách tính chu vi hình thang
P = a + b + c + d
Chu vi hình thang bằng tổng độ dài của hai đáy và cạnh bên.
Hình thang vuông: Có một cạnh bên vuông góc với hai đáy, cạnh bên đó chính là chiều cao hình thang vuông. Khi tính diện tích hình thang vuông ta tính như cách tìm hình thang.
Ví dụ cụ thể giả sử ta có hình thang ABCD với các cạnh AB = 8, cạnh đáy CD = 13, chiều cao giữa 2 cạnh đáy là 7 thì chúng ta sẽ có diện tích hình thang là:
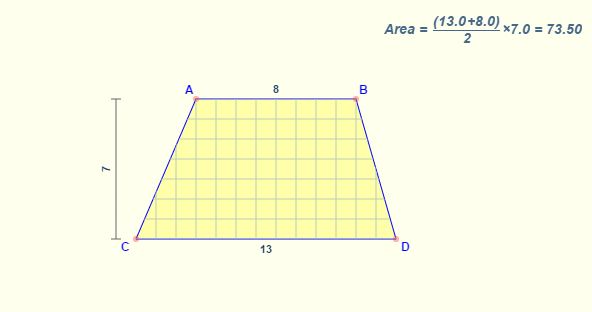
S(ABCD) = (8+13)/2 x 7 = 73.5
Tương tự ví dụ với trường hợp hình thang vuông chúng ta cũng tính tương tự
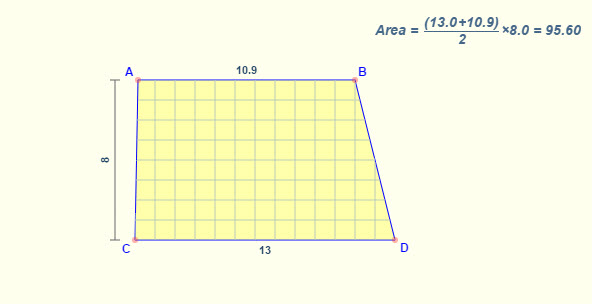
S(ABCD) = (AB + CD)/2 x AC = (10.9 + 13)/2 x 8 = 95.6
4. Tính diện tích hình thang khi biết 4 cạnh
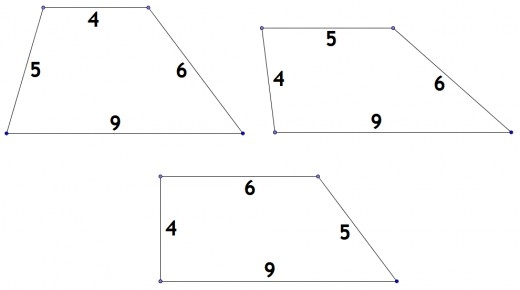
Thực tế nếu bài toán đưa ra câu hỏi cách tính 4 cạnh của hình thang khi biết 4 cạnh thì sẽ không có đáp án chính xác vì chỉ biết 4 cạnh thì có rất nhiều trường hợp xay ra và diện tích cũng khác nhau, các bạn có thể hình dung ví dụ hình thang dưới đây có 4 cạnh 4 5 6 9 có thể vẽ 3 dạng hình khác nhau với diện tích khác nhau.
Tuy nhiên nếu bài toán cho thêm vài dữ kiện ví dụ như tính diện tích hình thang khi biết độ dài 4 cạnh và có nõi rõ cạnh đáy là cạnh nào thì có thể tính được diện tích hình thang, ví dụ chúng tao có các cạnh đấy Q P, trong đó cạnh đáy P dài hơn và 2 cạnh bên R và S.
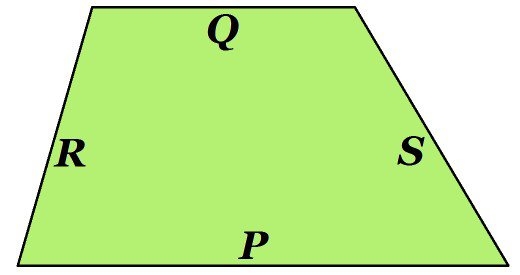
Thì có thể áp dụng công thức tính diện tích hình thang như sau:
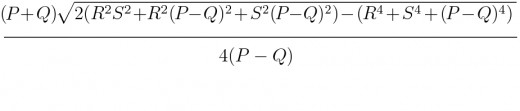
Ngoài ra trong trường hợp tính diện tích hình thang khi biết các cạnh các bạn có thể tách ra thành 2 tam giác và 1 hình chữ nhật hoặc kẻ thêm đường giao giữa 2 cạnh bên và áp dụng công thức Heron tính diện tích tam giác và suy ra được diện tích hình thang. Công thức trên cũng được hình thành từ cách này.
II. Các dạng bài tập liên quan đến hình thang
Dạng 1: Tính chu vi hình bình thang khi viết độ dài các đáy và cạnh bên
Ví dụ: Tính chu vi của hình thang, biết đáy lớn bằng 12 cm; đáy bé bằng 10 cm và hai cạnh bên lần lượt bằng 7 cm và 8 cm
Lời giải:
Chu vi hình thang là:
12 + 10 + 7 + 8 = 37 (cm)
Đáp số: 37cm
Ví dụ: Hình thang cân có độ dài hai cạnh đáy và chiều cao lần lượt là 40m, 30m và 25m có chu vi là:
| A. 95m | B. 120m |
| C. 2 875m | D. 2 8750m |
Lời giải:
Chu vi hình thang cân là
40 + 30 + (2 x25)
= 40 + 30 + 50
= 120m
Đáp số: 120m
Dạng 2: Tính độ dài cạnh bên của hình thang cân khi biết chu vi
Ví dụ: Tính độ dài của hình thang có hai cạnh bên bằng nhau biết chu vi của hình thang bằng 68cm và độ dài hai cạnh đáy lần lượt là 20cm và 26cm.
Lời giải:
Tổng độ dài hai cạnh bên của hình thang là:
68 – 20 – 26 = 22 (cm)
Độ dài cạnh bên của hình thang là:
22 : 2 = 11 (cm)
Đáp số: 11cm
Ví dụ: Một hình thang cân có chu vi bằng chu vi hình vuông cạnh 4cm.
Độ dài hai đáy của hình thang cân là 3cm, 5cm.
Độ dài cạnh bên của hình thang cân đó là ... cm.
Lời giải:
Chu vi của hình vuông cạnh 4cm là:
4 x 4 = 16 (cm)
Độ dài hai cạnh bên của hình thang là:
16 - 5 - 3 = 8 (cm)
Hai cạnh bên bằng nhau
Độ dài cạnh bên là:
8 : 2 = 4 (cm)
Đáp số: 4 cm
Ví dụ: Cho hình thang cân có tổng hai đáy bằng 18 dm và chu vi hình thang cân 340 cm. Độ dài cạnh bên của hình thang cân là:
| A. 8cm | В. 16dm |
| С. 8 dm | D. 16cm |
Lời giải:
Đổi 340 cm = 34 dm.
Tổng độ dài hai cạnh bên là: 34 – 18 = 16 dm.
Vạy độ dài cạnh bên của hình thang cân là: 16 : 2 = 8 dm.
Đáp số: 8dm
Dạng 3: Tính diện tích hình bình thang khi biết độ dài hai đáy và chiều cao
Ví dụ: Cho hình thang có độ dài đáy nhỏ bằng 5cm, đáy lớn bằng 10cm. Chiều cao của hình thang bằng 6cm. Tính diện tích của hình thang đó.
Lời giải:
Diện tích hình thang là:
(5 + 10) x 6 : 2 = 45 (cm2)
Đáp số: 45cm2
Ví dụ: Tính diện tích và chu vi hình thang cân có độ dài hai đáy là 4cm và 10cm; chiều cao 4cm; cạnh bên 5cm.
Lời giải:
Diện tích hình thang đó là:
(4 + 10) : 2 x 4 = 28(cm²)
Chu vi hình thang đó là:
4 + 10 + 5 x 2 = 24(cm)
Đáp số: 24cm
Dạng 4: Tính chiều cao khi biết độ dài hai đáy và diện tích
Ví dụ: Một hình thang vuông có diện tích bằng 14dm2, đáy bé bằng 2dm và đáy lớn bằng 5dm. Tính độ dài chiều cao của hình thang vuông đó.
Từ công thức tính diện tích hình thang, ta suy ra được công thức tính chiều cao của hình thang, đó là: h = S x 2 : (a + b) (Để tính chiều cao của hình thang, ta lấy diện tích chia cho trung bình cộng của hai đáy.)
Lời giải:
Độ dài chiều cao của hình thang là:
14 x 2 : (2 + 5) = 4 (dm)
Đáp số: 4dm
Dạng 5: Tính diện tích hình thang khi chưa biết độ dài hai đáy và chiều cao
Ví dụ: Một hình thang có chiều cao bằng 56cm. Đáy lớn hơn đáy bé 24cm và đáy bé bằng 2/5 đáy lớn. Tính diện tích hình thang.
Lời giải:
Hiệu số phần bằng nhau là:
5 – 2 = 3 (phần)
Độ dài đáy lớn là:
24 : 3 x 5 = 40 (cm)
Độ dài đáy bé là:
40 – 24 = 16 (cm)
Diện tích hình thang là:
(16 + 40) x 56 : 2 = 1568 (cm2)
Đáp số: 1568cm2
III. Bài tập vận dụng
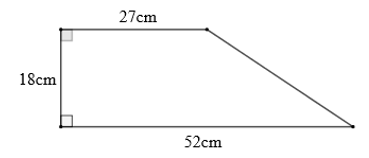
Bài 1 : Tính diện tích của hình thang sau
Giải:
Diện tích của hình thang là: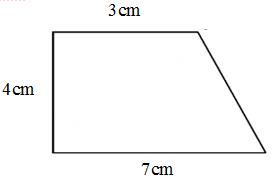
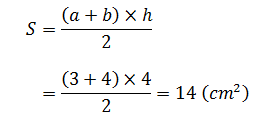
Bài 2 : Có một mạnh ruộng hình thang với độ dài hai đáy lần lượt là ứng là 110m và 90,2m. Chiều cao bằng tổng trung bình cộng của hai đáy. Hãy tính diện tích thửa ruộng đó.
Giải:
– Chiều cao của thửa ruộng đó là : (110 + 90,2) : 2 = 100,1 (m)
– Diện tích của thửa ruộng đó là :
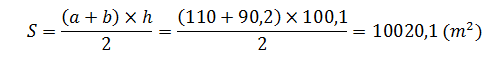
Bài 3 : Cho một thửa ruộng hình thang có đáy lớn bằng 120m, đáy bé bằng 2/3 đáy lớn. Đáy bé dài hơn chiều cao 5m. Trung bình cứ 100m2 thu hoạch được 64,5kg thóc. Hãy tính số ki – lô – gam thóc thu hoạch được trên thửa ruộng đó?
Giải:
– Độ dài đáy bé của thửa ruộng đó là:
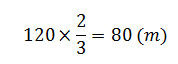
– Độ dài chiều cao của thửa ruộng đó là:
80 – 5 = 75 (m)
– Diện tích của thửa ruộng đó là:
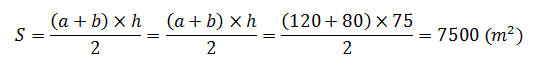
– Số ki – lô – gam thóc thu hoạch được trên thửa ruộng đó là :
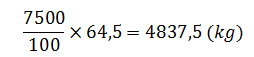
Câu 4: Điền số thích hợp vào ô trống:
Diện tích hình thang có đáy lớn là 45dm, đáy bé là 25dm và chiều cao là 2m là 
Giải:
Đổi 2m = 20dm
Diện tích hình thang đó là:
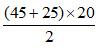
Đáp số: 700dm2
Vậy đáp án đúng điền vào ô trống là 700.
Câu 5: Điền số thích hợp vào ô trống:
Cho hình thang như hình vẽ:
Diện tích hình thang đã cho là 
Giải:
Diện tích hình thang đó là:
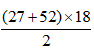
Đáp số: 711cm2.
Vậy đáp án đúng điền vào ô trống là 711
Cho hình thang ABCD có đáy lớn AB = 8cm, đáy nhỏ CD = 4cm và chiều cao h = 6cm. Hãy tính chu vi và diện tích của hình thang này.
Giải:
Đầu tiên, ta cần tính độ dài hai cạnh bên của hình thang. Ta có:
AD = BC = (đáy lớn - đáy nhỏ) / 2 = (8 - 4) / 2 = 2cm
Tiếp theo, ta tính chu vi của hình thang:
Chu vi = AB + BC + CD + AD = 8 + 2 + 4 + 2 = 16cm
Để tính diện tích của hình thang, ta sử dụng công thức:
Diện tích = (đáy lớn + đáy nhỏ) * chiều cao / 2 = (8 + 4) * 6 / 2 = 36cm^2
Vậy, chu vi của hình thang là 16cm và diện tích là 36cm^2.
Bài 7:
Cho hình thang ABCD có chiều cao h = 10cm và đáy lớn AB là gấp đôi đáy nhỏ CD. Biết rằng chu vi của hình thang là 36cm. Hãy tính độ dài các cạnh của hình thang này.
Giải:
Gọi x là độ dài đáy nhỏ CD. Theo đề bài, ta có: AB = 2CD.
Ta nhận thấy chu vi của hình thang là tổng độ dài các cạnh, vậy ta có:
AB + BC + CD + DA = 36
Thay các giá trị vào, ta có:
2x + BC + x + BC = 36
3x + 2BC = 36
Do đáy lớn AB là gấp đôi đáy nhỏ CD nên có: AB = 2x và BC = x.
Thay vào công thức trên, ta có:
3x + 2x = 36
5x = 36
x = 7.2
Vậy, độ dài của đáy nhỏ là x = 7.2cm và đáy lớn là AB = 2x = 2 * 7.2 = 14.4cm.
Do đáy lớn AB là gấp đôi đáy nhỏ CD nên ta có: AB = 2CD.
Thay giá trị của AB vào, ta có: 14.4 = 2CD
CD = 14.4 / 2 = 7.2cm.
Vậy, độ dài của các cạnh là AB = 14.4cm, BC = 7.2cm, CD = 7.2cm và DA = 14.4cm.