Bất đẳng thức Cô-si và hệ quả chi tiết nhất
Lí thuyết tổng hợp
- Định lí: Trung bình nhân của hai số không âm nhỏ hơn hoặc bằng trung bình cộng của chúng.
√ab≤a+b2∀a,b≥0
Đẳng thức √ab=a+b2 xảy ra khi và chỉ khi a = b.
- Các hệ quả:
+ Tổng của một số dương với nghịch đảo của nó lớn hơn hoặc bằng 2.
a+1a≥2,∀a>0
+ Nếu x, y cùng dương và có tổng không đổi thì tích (xy) lớn nhất khi và chỉ khi x = y.
+ Trong tất cả các hình chữ nhật có cùng chu vi, hình vuông có diện tích lớn nhất.
+ Nếu x, y cùng dương và có tích không đổi thì tổng (x + y) nhỏ nhất khi và chỉ khi x = y.
+ Trong tất cả các hình chữ nhật có cùng diện tích, hình vuông có chu vi nhỏ nhất.
Các công thức
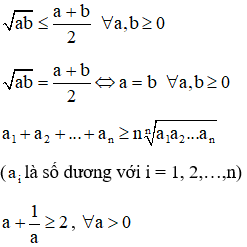
∀x,y>0 , nếu (x+y) không đổi thì (x.y)max⇔x=y.
∀x,y>0 , nếu (x.y) không đổi thì (x+y)min⇔x=y.
Bài tập vận dụng (có đáp án)
Bài 1: Cho a, b là số dương thỏa mãn a2+b2=2. Chứng minh rằng: (ab+ba)(ab2+ba2)≥4.
Lời giải:
Khi a, b là số dương ⇒ab>0, ba>0, ab2>0,ba2>0
Áp dụng bất đẳng thức Cô-si ta có:
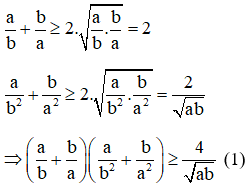
Mặt khác ta có:
2=a2+b2≥2√a2b2=2ab
⇒ab≤1 (2)
Từ (1) và (2) ta có: (ab+ba)(ab2+ba2)≥4 (điều cần phải chứng minh)
Đẳng thức xảy ra khi và chỉ khi a = b = 1.
Bài 2: Cho a, b, c, d là số dương. Chứng minh rằng: (ab3+bc3+cd3+da3)(a+b)(c+d)≥16
Lời giải:
Vì a, b, c, d là số dương nên ta có: ab3>0, bc3>0, cd3>0,da3>0
Áp dụng Bất đẳng thức Cô-si cho bốn số dương ta có:
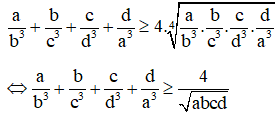
Lại có, do a, b, c, d dương nên:
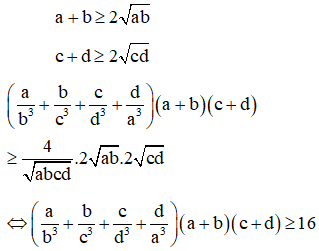
(điều cần phải chứng minh).
Bài 3: Cho hai số dương c, d. Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của các biểu thức trong các trường hợp sau:
a) c + d = 6 luôn không đổi, tìm giá trị lớn nhất của biểu thức A = (c + d).cd ;
b) c.d = 5 luôn không đổi, tìm giá trị nhỏ nhất của biểu thức B=c+dc2d2.
Lời giải:
a)
Ta có: A = (c + d).cd = 6cd vì (c + d) = 6 luôn không đổi.
Áp dụng hệ quả của bất đẳng thức Cô-si ta có:
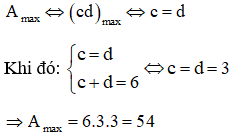
Vậy giá trị lớn nhất của A là 54 khi c = d = 3.
b)
Ta có: B=c+dc2d2=c+d52=c+d25 vì c.d = 5 luôn không đổi.
Áp dụng hệ quả của bất đẳng thức Cô-si ta có:
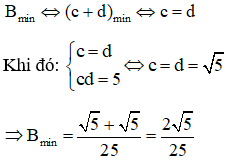
Vậy giá trị nhỏ nhất của B là 2√525 khi c = d = √5.
Bài 4: Tìm giá trị nhỏ nhất của biểu thức với x > 0
Lời giải:
Áp dụng bất đẳng thức Cô si cho hai số x > 0 và ta có:
Dấu “=” xảy ra khi và chỉ khi (do x > 0)
Vậy min
Bài 5: Cho x > 0, y > 0 thỏa mãn điều kiện . Tìm giá trị lớn nhất của biểu thức
Lời giải:
Áp dụng bất đẳng thức Cô si cho hai số x > 0, y > 0 ta có:
Lại có, áp dụng bất đẳng thức Cô si cho hai số x > 0, y > 0 ta có:
Dấu “=” xảy ra khi và chỉ khi
Vậy minA = 4 khi và chỉ khi x = y = 4
Bài 6: Chứng minh với ba số a, b, c không âm thỏa mãn a + b + c = 3 thì:
Nhận xét: Bài toán đạt được dấu bằng khi và chi khi a = b = c = 1. Ta sẽ sử dụng phương pháp làm trội làm giảm như sau:
Lời giải:
Áp dụng bất đẳng thức Cô si cho ba số a, b, c không âm có:
Tương tự ta có và
Cộng vế với vế ta có:
Dấu “=” xảy ra khi và chỉ khi a = b = c = 1
Bài tập tự luyện
Bài 1: Cho a, b, c là số dương thỏa mãn a2+b2+c2=3. Chứng minh rằng: a2b+b2c+c2a≤3.
Bài 2: Cho a, b, c là số dương. Chứng minh rằng abc+bca+acb.
Bài 3: Tìm giá trị nhỏ nhất của các biểu thức sau:
a, với x > 0
(gợi ý: biến đổi rồi áp dụng bất đẳng thức Cô si)
b, với x > 0
c, với x > 2
(gợi ý: biến đổi rồi áp dụng bất đẳng thức Cô si)
Bài 4: Tìm giá trị nhỏ nhất của biểu thức với x > y > 0
(gợi ý: biến đổi )
Bài 5: Với a, b, c là các số thực không âm, chứng minh:
(gợi ý áp dụng bất đẳng thức Cô si cho ba số a, b, c không âm)
Bài 6: Cho ba số thực dương a, b, c thỏa mãn a + b + c = 3. Chứng minh rằng:
(gợi ý sử dụng phương pháp làm trội)
Xem thêm tổng hợp các dạng toán lớp 10 đầy đủ, chi tiết và hay khác:
200 Bài tập Bất phương trình bậc nhất hai ẩn (có đáp án năm 2023)
100 Bài tập hệ bất phương trình bậc nhất hai ẩn (có đáp án năm 2023)
500 Bài tập Toán 10 bất phương trình và hệ phương trình bậc nhất hai ẩn (có đáp án năm 2023)




