90 Bài tập về hai mặt phẳng vuông góc (có đáp án năm 2024) - Toán 11

Bài giảng Toán 11 Bài 4: Hai mặt phẳng vuông góc

Kiến thức cần nhớ

I. Góc giữa hai mặt phẳng

1. Định nghĩa:

Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.

- Nếu hai mặt phẳng song song hoặc trùng nhau thì ta nói rằng góc giữa hai mặt phẳng đó bằng 0⁰.

2. Cách xác định góc giữa hai mặt phẳng cắt nhau.

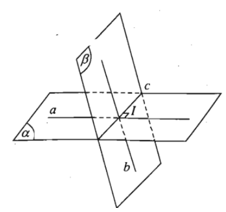
- Giả sử 2 mặt phẳng (α) và (β) cắt nhau theo giao tuyến c. Từ một điểm I bất kì trên c ta dựng trong (α) đường thẳng a vuông góc với c và dựng trong (β) đường thẳng b vuông góc với c.

- Khi đó, góc giữa hai mặt phẳng (α) và (β) là góc giữa hai đường thẳng a và b.

Ví dụ 1. Cho hình chóp S. ABC có $SA\perp \left(ABC\right);AB\perp BC$, gọi I  là trung điểm BC. Ta xác định góc giữa hai mặt phẳng ( SBC) và ( ABC) :

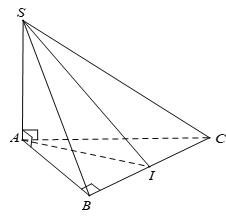
Ta có:

$$\begin{gathered} BC\perp SA,BC\perp AB \\ \Rightarrow BC\perp \left(SAB\right)\Rightarrow BC\perp SB \\ \Rightarrow \left\{\begin{array}{c}\left(SBC\right)\cap \left(ABC\right)=BC\\ AB\perp BC,AB\subset \left(ABC\right)\\ SB\perp BC,SB\subset \left(SBC\right)\end{array}\right. \\ \Rightarrow \widehat{\left(\left(SBC\right),\left(ABC\right)\right)}=\widehat{SBA} \end{gathered}$$

3. Diện tích hình chiếu của một đa giác.

Cho đa giác H nằm trong mặt phẳng (α) có diện tích S và H’ là hình chiếu vuông góc của H lên mp(β).

Khi đó, diện tích S’ của H’ được tính theo công thức:

$S\text{'}=\text{\hspace{0.17em}}S.c\text{os}\phi$ với là góc giữa (α)  và (β).

II. Hai mặt phẳng vuông góc.

1. Định nghĩa.

Hai mặt phẳng gọi là vuông góc với nhau nếu góc giữa hai mặt phẳng đó là góc vuông.

Nếu hai mặt phẳng (α) và (β) vuông góc với nhau ta kí hiệu: $\left(\alpha \right)\perp \left(\beta \right)$.

2. Các định lí.

- Định lí 1.

Điều kiện cần và đủ để hai mặt phẳng vuông góc với nhau là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

- Hệ quả 1.

Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến thì vuông góc với mặt phẳng kia.

- Hệ quả 2.

Cho hai mặt phẳng (α) và (β) vuông góc với nhau. Nếu từ một điểm thuộc mặt phẳng (α) ta dựng một đường thẳng vuông góc với mặt phẳng (β) thì đường thẳng này nằm trong mặt phẳng (α).

Ví dụ 2. Cho tứ diện ABCD có . Trong  tam  giác  BDC vẽ các đường cao BE và DF cắt nhau ở O. Trong( ADC) vẽ  tại K. Chứng minh

a) $\left(ADC\right)\perp \left(ABE\right)$

b) $\left(ADC\right)\perp \left(DF\text{}K\right)$

c) $\left(BCD\right)\perp \left(ABE\right)$

Lời giải:

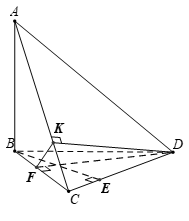
a) Ta có 

$\begin{array}{l}\left\{\begin{array}{l}CD\perp BE\\ CD\perp AB\end{array}\right.\Rightarrow \left\{\begin{array}{l}CD\perp \left(ABE\right)\\ CD\subset \left(ADC\right)\end{array}\right.\\ \Rightarrow \left(ADC\right)\perp \left(ABE\right)\\ \end{array}$

b) Ta có:

$\left.\begin{array}{l}DF\perp BC\\ DF\perp AB\end{array}\right\}\Rightarrow DF\perp \left(ABC\right)$

Mà $SC\subset \left(ABC\right)\Rightarrow \left\{\begin{array}{l}DF\perp AC\\ DK\perp AC\end{array}\right.$

$\Rightarrow \left.\begin{array}{l}AC\perp \left(DFK\right)\\ AC\subset \left(ADC\right)\end{array}\right\}\Rightarrow \left(ADC\right)\perp \left(DFK\right)$

c) Ta có 

$$\begin{gathered} \left.\begin{array}{l}CD\perp BE\\ CD\perp AB\end{array}\right\}\Rightarrow CD\perp \left(ABE\right) \\ CD\subset \left(BDC\right)\Rightarrow \left(BDC\right)\perp \left(ABE\right) \end{gathered}$$

III. Hình lăng trụ đứng, hình hộp chữ nhật, hình lập phương.

1. Định nghĩa. Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với các mặt đáy. Độ dài cạnh bên được gọi là chiều cao của hình lăng trụ đứng.

- Hình lăng trụ đứng có đáy là tam giác, tứ giác, ngũ giác… được gọi là hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác, hình lăng trụ đứng ngũ giác…

- Hình lăng trụ đứng có đáy là một đa giác đều được gọi là hình lăng trụ đều.

Ta có các loại hình lăng trụ đều như  lăng trụ tam giác đều, lăng trụ tứ giác đều..

- Hình lăng trụ đứng có đáy là hình bình hành được gọi là hình hộp đứng.

- Hình lăng trụ đứng có đáy là hình chữ nhật được gọi là hình hộp chữ nhật.

- Hình lăng trụ đứng có đáy là hình vuông và các mặt bên đều là hình vuông được gọi là hình lập phương.

2. Nhận xét

Các mặt bên của hình lăng trụ đứng luôn luôn vuông góc với mặt phẳng đáy và là những hình chữ nhật.

IV. Hình chóp đều và hình chóp cụt đều.

1. Hình chóp đều.

 Cho hình chóp đỉnh S có đáy là đa giác A₁A₂…A_n và H là hình chiếu vuông góc của S trên mặt phẳng đáy (A₁A₂…A_n). Khi đó, đoạn thẳng SH gọi là đường cao của hình chóp và H là chân đường cao của hình chóp.

- Định nghĩa. Một hình chóp được gọi là hình chóp đều nếu nó có đáy là một đa giác đều và có chân đường cao trùng với tâm của đa giác đáy.

- Nhận xét:

a) Hình chóp đều có các mặt bên là những tam giác cân bằng nhau. Các mặt bên tạo với mặt đáy các góc bằng nhau.

b) Các cạnh bên của hình chóp đều tạo với mặt đáy các góc bằng nhau.

2. Hình chóp cụt đều.

- Định nghĩa: Phần của hình chóp đều nằm giữa đáy và một thiết diện song song với đáy cắt các cạnh bên của hình chóp đều được gọi là hình chóp cụt đều.

- Ví dụ 3: Hình ABCD.A’B’C’D’ ở hình dưới là một hình chóp cụt đều. Hai đáy của hình chóp cụt đều là 2 đa giác đều và đồng dạng với nhau.

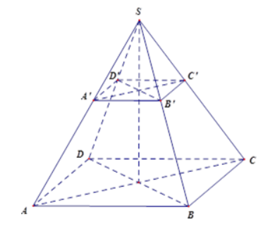
- Nhận xét. Các mặt bên của hình chóp cụt đều là những hình thang cân và các cạnh bên của hình chóp cụt đều có độ dài bằng nhau.

Các dạng toán về hai mặt phẳng vuông góc

(Xem chi tiết trong file đính kèm)

Dạng 1. Câu hỏi lý thuyết.

Dạng 2. Chứng minh hai mặt phẳng vuông góc.

Dạng 3. Tính góc giữa hai mặt phẳng.

Dạng 4. Thiết diện.

Bài tập (có hướng dẫn giải)

1. Bài tập vận dụng

Bài 1. Cho tứ diện ABCD có hai mặt phẳng (ABC) và ( ABD) cùng vuông góc với ( DBC). Gọi BE và DF là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Chứng minh:

a) $\left(ABE\right)\perp \left(ADC\right)$

b) $\left(ABC\right)\perp \left(\text{}D\text{}FK\right)$

c) $\left(D\text{}FK\right)\perp \left(ADC\right)$

Lời giải:

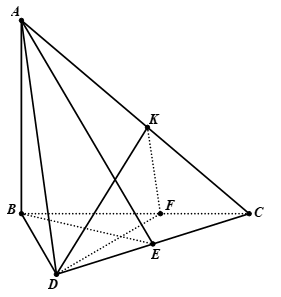
a) Vì hai mặt phẳng ( ABC) và ( ABD) cùng vuông góc với ( DBC) nên

Ta có:

$\begin{array}{l}\left\{\begin{array}{c}CD\perp BE\\ CD\perp AB\end{array}\right.\\ \Rightarrow CD\perp \left(ABE\right)\Rightarrow \left(ABE\right)\perp \left(ADC\right)\end{array}$

b) Vì:

$\begin{array}{l}\left\{\begin{array}{c}DF\perp BC\\ DF\perp AB\end{array}\right.\\ \Rightarrow DF\perp \left(ABC\right)\Rightarrow \left(ABC\right)\perp \left(DFK\right)\end{array}$

c) Ta có:

$\begin{array}{l}\left\{\begin{array}{c}AC\perp DK\\ AC\perp DF\end{array}\right.\\ \Rightarrow AC\perp \left(DFK\right)\Rightarrow \left(DFK\right)\perp \left(ADC\right)\end{array}$

Bài 2. Cho tứ diện ABCD có AC= AD và BC= BD. Gọi I  là trung điểm của CD.

a) Chứng minh: $\left(BCD\right)\perp \left(AIB\right)$ và $\left(ACD\right)\perp \left(AIB\right)$

b) Xác định góc giữa hai mặt phẳng ( ACD) và ( BCD)

Lời giải:

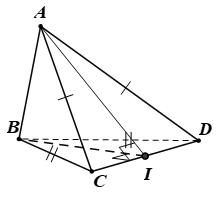
a) Tam giác BCD cân tại B có I trung điểm đáy CD

$\Rightarrow CD\perp BI$ (1)

Tam giác CAD  cân tại A có I trung điểm đáy CD

$\Rightarrow CD\perp AI$ (2)

Từ  (1) và (2)  $\Rightarrow CD\perp \left(ABI\right)$

Suy ra: $\left(BCD\right)\perp \left(AIB\right)$ và $\left(ACD\right)\perp \left(AIB\right)$

b) Góc giữa hai mặt phẳng ( ACD) và ( BCD)  là

$\left(\left(ACD\right);\left(BCD\right)\right)=(BI;AI)=\widehat{AIB}$

Bài 3. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Tính của góc giữa một mặt bên và một mặt đáy.

Lời giải:

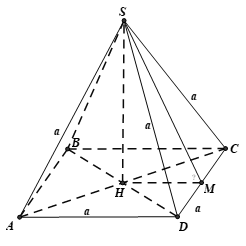
Gọi H là giao điểm của AC và BD.

+ Do S.ABCD là hình chóp tứ giác đều  nên $SH\perp \left(ABCD\right)$.

Ta có: $\left(SCD\right)\cap \left(ABCD\right)=CD$.

Gọi M là trung điểm CD.

+  Tam  giác  SCD là cân  tại S ; và tam  giác CHD cân tại H ( tính chất hình vuông).

$\Rightarrow SM\perp CD;HM\perp CD$

$\Rightarrow \left(\left(SCD\right),\left(ABCD\right)\right)=\left(SM,HM\right)$$=\widehat{SMH}=\alpha$

Từ giả thiết suy ra tam giác  SCD là tam giác đều cạnh a có SM là đường trung tuyến $\Rightarrow SM=\frac{a\sqrt{3}}{2}$.

$\Rightarrow \cos \alpha =\frac{HM}{SM}=\frac{\frac{a}{2}}{\frac{a\sqrt{3}}{2}}=\frac{1}{\sqrt{3}}$

2. Bài tập tự luyện

(Xem trong file đính kèm bên dưới)