70 Bài tập về Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác (có đáp án năm 2024) - Toán 7

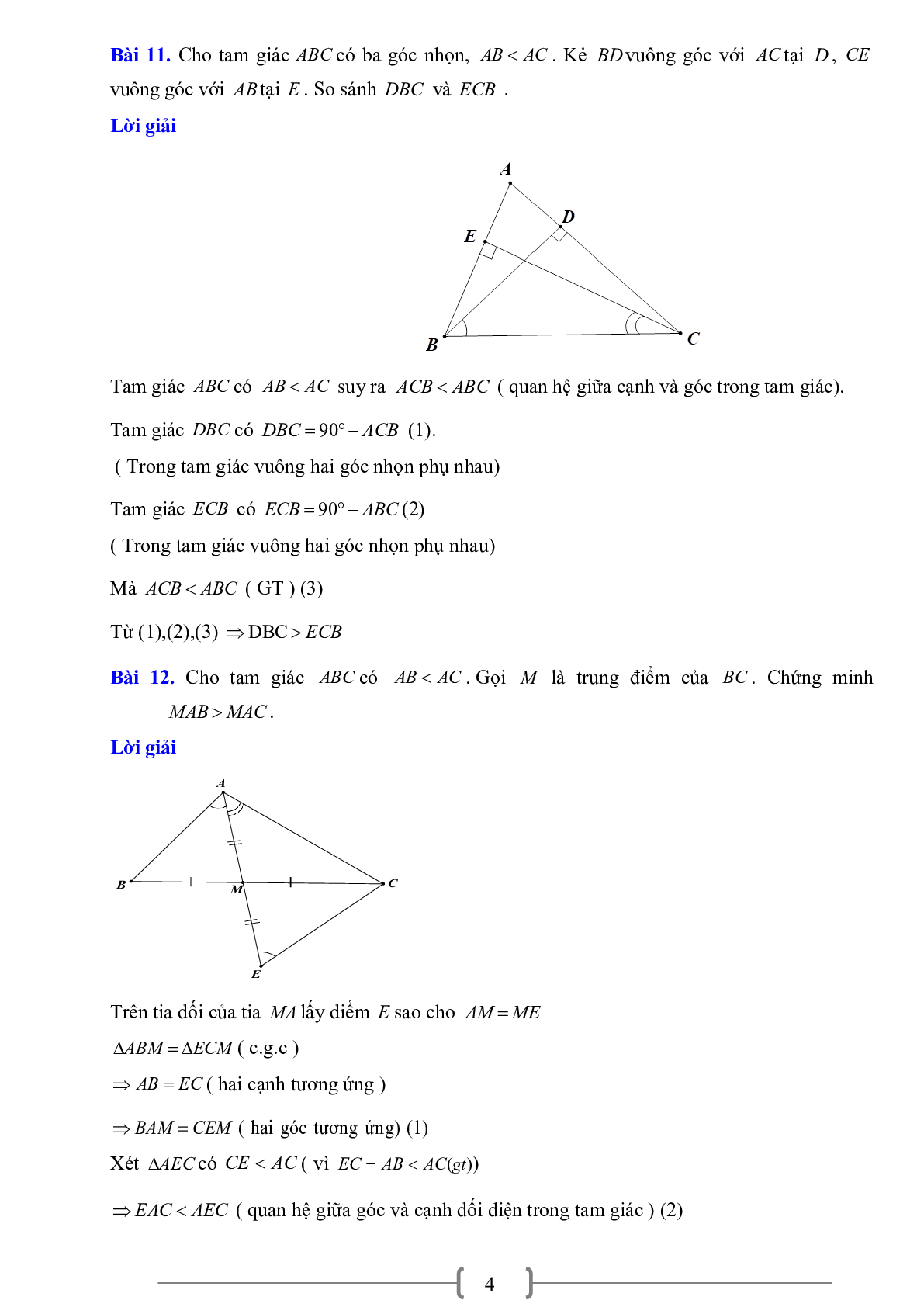
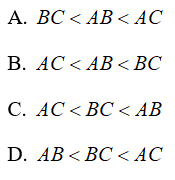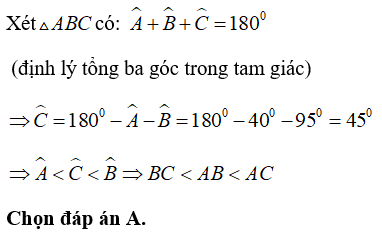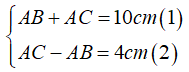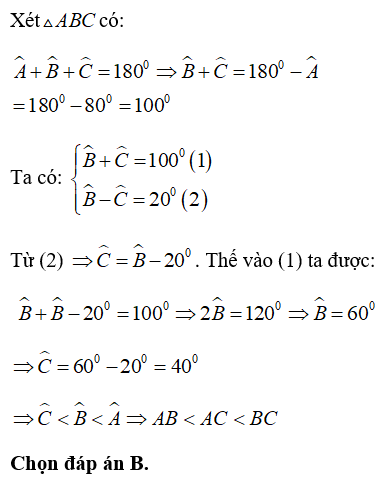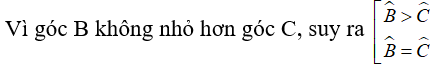 Bài tập về Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác

Kiến thức cần nhớ

1. Quan hệ giữa góc và cạnh đối diện trong một tam giác

1.1. Góc đối diện với cạnh lớn hơn

– Trong tam giác ABC:

• Góc A được gọi là góc đối diện với cạnh BC;

• Góc B được gọi là góc đối diện với cạnh CA;

• Góc C được gọi là góc đối diện với cạnh AB.

– Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.

Trong tam giác ABC, nếu AC > AB thì $\widehat{\mathrm{B}}>\widehat{\mathrm{C}}.$

Ví dụ: Cho tam giác ABC có AC = 4 cm, BC = 5 cm. So sánh góc A và góc B.

Hướng dẫn giải

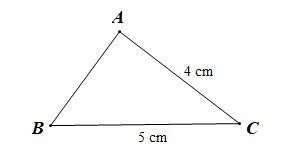
Xét tam giác ABC có BC > AC (5 cm > 4 cm)

Mà $\widehat{\mathrm{A}}$ đối diện với cạnh BC, $\widehat{\mathrm{B}}$ đối diện với cạnh AC.

Nên $\widehat{\mathrm{A}}>\widehat{\mathrm{B}}$ (trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn)

Vậy $\widehat{\mathrm{A}}>\widehat{\mathrm{B}}$.

1.2. Cạnh đối diện với góc lớn hơn

– Trong tam giác ABC:

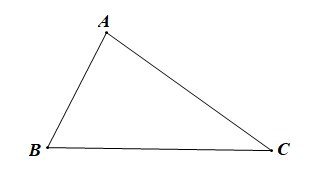
• Cạnh BC được gọi là cạnh đối diện với góc A;

• Cạnh CA được gọi là cạnh đối diện với góc B;

• Cạnh AB được gọi là cạnh đối diện với góc C.

– Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.

Trong tam giác ABC, nếu $\widehat{\mathrm{B}}>\widehat{\mathrm{C}}$ thì AC > AB.

– Nhận xét:

+ Trong tam giác vuông, cạnh huyền là cạnh lớn nhất.

+ Trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất.

Ví dụ: So sánh các cạnh của tam giác trong các hình vẽ sau:

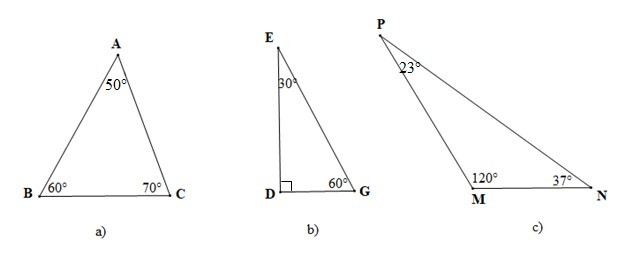
Hướng dẫn giải

• Hình a)

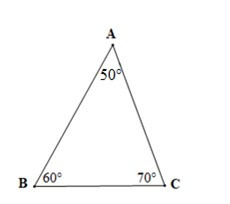
Xét tam giác ABC có $\widehat{\mathrm{C}}>\widehat{\mathrm{B}}>\widehat{\mathrm{A}}$ (70° > 60° > 50°)

Nên AB > AC > BC (trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn)

Vậy AB > AC > BC.

• Hình b)

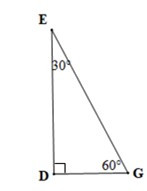
Vì DDEG vuông tại D nên cạnh huyển EG là cạnh lớn nhất (trong tam giác vuông, cạnh huyền là cạnh lớn nhất)

Xét DDEG có $\widehat{\mathrm{G}}>\widehat{\mathrm{E}}$ (60° > 30°)

Nên DE > DG (trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn)

Vậy EG > DE > DG.

• Hình c)

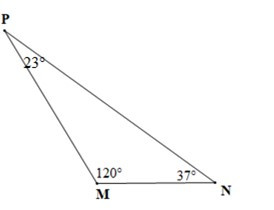
Vì DMNP có $\widehat{\mathrm{M}}=120°$ nên là tam giác tù.

Do đó cạnh NP là cạnh lớn nhất (Trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất)

Xét DMNP có $\widehat{\mathrm{N}}>\widehat{\mathrm{P}}$ (37° > 23°)

Nên PM > MN (trong một tam góc, cạnh đối diện với góc lớn hơn là cạnh lớn hơn)

Vậy NP > PM > MN.

2. Bất đẳng thức tam giác

– Trong một tam giác, tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại.

Trong tam giác ABC, ta có: AB + BC > AC; AB + AC > BC; AC + BC > AB.

Các bất đảng thức này gọi là các bất đẳng thức tam giác.

– Nhận xét: Trong một tam giác, hiệu độ dài hai cạnh bất kì nhỏ hơn độ dài cạnh còn lại.

Ví dụ: Dựa vào bất đẳng thứ tam giác, kiểm tra xem bộ ba độ dài 2 cm, 8 cm, 6 cm và 3 cm, 5 cm, 7 cm có thể là độ dài ba cạnh của một tam giác không? Vì sao?

Hướng dẫn giải

+) Xét bộ ba độ dài: 2 cm, 8 cm, 6 cm.

Ta có: 2 + 6 = 8 không thỏa mãn bất đẳng thức tam giác nên bộ ba độ dài 2 cm, 8 cm, 6 cm không thể là độ dài ba cạnh của một tam giác.

+) Xét bộ ba độ dài: 3 cm, 5 cm, 7 cm

Ta có: $\left\{\begin{array}{l}3+5=8>7\\ 3+7=10>5\\ 5+7=12>3\end{array}\right.$ thỏa mãn bất đẳng thức tam giác nên bộ ba độ dài 3 cm, 5 cm, 7 cm là độ dài ba cạnh của một tam giác.

Các dạng bài tập Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác

Dạng 1. So sánh các góc trong một tam giác

Phương pháp giải

+ TH1: Nếu các góc cần so sánh nằm trong cùng một tam giác thì ta áp dụng định lí 1: So sánh các cạnh đối diện với các góc đó.

+ TH2: Nếu các góc cần so sánh không cùng nằm trong cùng một tam giác Thì ta dùng góc trung gian để so sánh

Dạng 2. So sánh các cạnh trong một tam giác

Phương pháp giải

+ TH1: Nếu các cạnh cần so sánh nằm trong cùng một tam giác thì ta áp dụng định lí 2: So sánh các góc đối diện với các cạnh đó

+ TH2: Nếu các góc cần so sánh không cùng nằm trong cùng một tam giác Thì ta dùng góc trung gian để so
sánh

Bài tập tự luyện

1. Bài tập vận dụng

A. Bài tập tự luận

Bài 1. Cho tam giác ABC nhọn. So sánh độ dài mỗi cạnh với nửa chu vi của tam giác đó.

Hướng dẫn giải

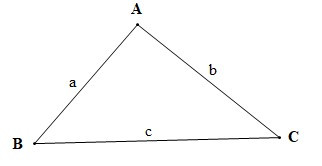
Gọi độ dài các cạnh của tam giác ABC là a, b, c (a, b, c > 0) (hình vẽ).

• Theo bất đẳng thức trong tam giác ta có a < b + c

Nên a + a < b + c + a

Hay 2.a < b + c + a

Suy ra  a < $\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}$

• Theo bất đẳng thức trong tam giác ta có b < a + c

Nên b + b < b + c + a

Hay 2.b < b + c + a

Suy ra b < $\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}$

• Theo bất đẳng thức trong tam giác ta có c < a + b

Nên c + c < b + c + a

Hay 2.c < b + c + a

Suy ra c < $\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}$

Vây độ dài một cạnh của tam giác luôn nhỏ hơn nửa chu vi của tam giác đó.

Bài 2. Cho tam giác MNP có góc M là góc tù. Trên cạnh MN lấy điểm D (D khác M, N), trên MP lấy điểm E (E khác M, P). So sánh DE và NP.

Hướng dẫn giải

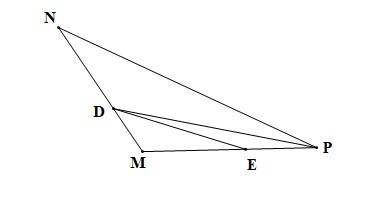
Vì $\widehat{\mathrm{PE}\text{D}}$ là góc ngoài của tam giác DME nên $\widehat{\mathrm{PE}\text{D}}=\widehat{\text{EDM}}+\widehat{\mathrm{M}}$

Mà $\widehat{\mathrm{M}}$ là góc tù (giả thiết) nên $\widehat{\mathrm{PE}\text{D}}$ là góc tù.

Xét tam giác DEP có $\widehat{\mathrm{PE}\text{D}}$ là góc tù, DP là cạnh đối diện với $\widehat{\mathrm{PE}\text{D}}$

Suy ra DE < DP (trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất).

Vì $\widehat{\mathrm{N}\text{D}\mathrm{P}}$ là góc ngoài của tam giác DPM nên $\widehat{\mathrm{N}\text{D}\mathrm{P}}=\widehat{\mathrm{DPM}}+\widehat{\mathrm{M}}$

Mà $\widehat{\mathrm{M}}$là góc tù (giả thiết) nên $\widehat{\mathrm{N}\text{D}\mathrm{P}}$ là góc tù.

Xét tam giác DNP có $\widehat{\mathrm{N}\text{D}\mathrm{P}}$ là góc tù, NP là cạnh đối diện với $\widehat{\mathrm{N}\text{D}\mathrm{P}}$

Suy ra DP < NP (trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất).

Lại có DE < DP (chứng minh trên).

Suy ra DE < DP < NP.

Vậy DE < NP.

Bài 3. Ba thành phố A, B, C trên bản đồ là ba đỉnh của một tam giác được mô tả như hình vẽ dưới đây, trong đó AB = 20 km, AC = 50 km.

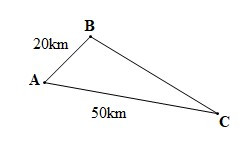
Nếu đặt ở C máy phát sóng truyền thanh có bán kính hoạt động bằng 30 km thì ở hai thành phố A và B có nhận được tín hiệu không ? Vì sao ?

Hướng dẫn giải

Xét tam giác ABC có

AC – AB < BC < AC + AB (bất đẳng thức trong tam giác)

Hay 50 – 20 < BC < 50 + 20

Suy ra 30 < BC < 70

Nếu máy phát sóng đặt ở thành phố C có bán kính hoạt động bằng 30 km thì ở thành phố B sẽ không nhận được tín hiệu vì BC > 30 km

Nếu máy phát sóng đặt ở thành phố C có bán kính hoạt động bằng 30 km thì ở thành phố A sẽ không nhận được tín hiệu vì AC = 50 km > 30 km

Vậy nếu máy phát sóng truyền thanh đặt ở thành phố C có bán kính hoạt động 30 km thì ở hai thành phố A và B đều không nhận được tín hiệu.

 Bài tập trắc nghiệm

Câu 1. Cho tam giác DEG có DE = 5 cm, EG = 7 cm, DG = 8 cm. Khẳng định nào sau đây là đúng?

A. Góc D là góc nhỏ nhất trong tam giác DEG;                

B. Góc E là góc nhỏ nhất trong tam giác DEG;                 

C. Góc G là góc nhỏ nhất trong tam giác DEG;                

D. Góc D là góc lớn nhất trong tam giác DEG.

Hướng dẫn giải

Đáp án đúng là: C

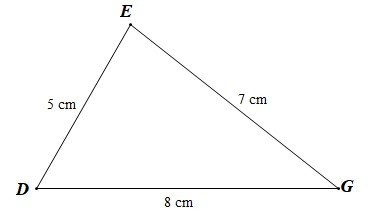
Vì tam giác DEG có DG > EG > DE (8 cm > 7 cm > 5 cm) nên theo quan hệ giữa cạnh và góc trong tam giác ta có $\widehat{\mathrm{E}}>\widehat{\mathrm{D}}>\widehat{\mathrm{G}}$

Vậy góc G là góc nhỏ nhất và góc E là góc lớn nhất trong tam giác DEG.

Câu 2. Cho tam giác ABC có AB = 1 cm, AC = 4 cm. Độ dài cạnh BC có thể là:

A. BC = 2 cm;

B. BC = 3 cm;

C. BC = 4 cm;

D. BC = 5 cm.

Hướng dẫn giải

Đáp án đúng là: C

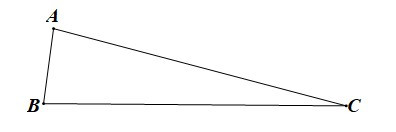
Áp dụng bất đẳng thức cho tam giác ABC ta có:

AC – AB < BC < AC + AB

Hay 4 – 1 < BC < 4 + 1

Suy ra 3 < BC < 5.

Trong các phương án thì chỉ có phương án C (BC = 4 cm) thỏa mãn điều kiện trên.

Vậy độ dài cạnh BC có thể là 4 cm.

Ta chọn phương án C.

Câu 3. Cho hình vẽ sau:

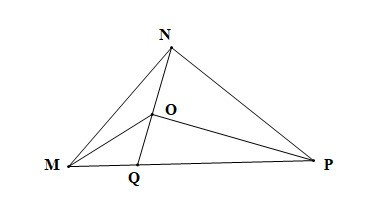
Khẳng định nào sau đây là đúng?

A. ON + OP > MN + MP;                   

B. ON + OP = MN + MP;         

C. ON + OP < MN + MP;         

D. ON + OP ≥ MN + MP.

Hướng dẫn giải

Đáp án đúng là: C

Xét DOPQ có OP < OQ + PQ (bất đẳng thức trong tam giác)

Xét DQNM có QN < MQ + MN (bất đẳng thức trong tam giác)

Suy ra OP + QN < OQ + PQ + MQ + MN

Hay OP + ON + OQ < OQ + MP + MN

Nên OP + ON  < MP + MN

Vậy ta chọn đáp án C.

Bài 4: Cho ΔABC có AC > BC > AB. Trong các khẳng định sau, câu nào đúng:

Lời giải:

Vì ΔABC có AC > BC > AB nên theo quan hệ giữa cạnh và góc trong tam giác ta có: ∠C < ∠A < ∠B

Chọn đáp án C.

Bài 5: Cho tam giác có: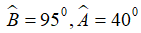. Hãy chọn câu trả lời đúng nhất:

Lời giải:

Bài 6: Ba cạnh của tam giác có độ dài là 6cm, 7cm, 8cm. Góc lớn nhất là góc:

A. Đối diện với cạnh có độ dài 6cm

B. Đối diện với cạnh có độ dài 7cm

C. Đối diện với cạnh có độ dài 8cm

D. Ba cạnh có độ dài bằng nhau

Lời giải:

Vì trong một tam giác, góc đối diện với cạnh lớn hơn thì lớn hơn mà cạnh 8cm là cạnh lớn nhất trong tam giác nên góc lớn nhất là góc đối diện với cạnh có độ dài 8cm

Chọn đáp án C.

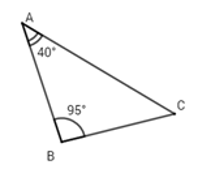
Bài 7: Cho ΔABC có AB + AC = 10cm; AC - AB = 4cm. So sánh ∠B và ∠C

Lời giải:

Xét ΔABC có:

Từ (1) ⇒ AC = 10 - AB. Thế vào (2) ta được: 10 - AB - AB = 4 ⇒ 2AB = 6 ⇒ AB = 3 cm

⇒ AC = 10 - 3 = 7cm

Vì 3 < 7 nên AB < AC ⇒ C^ < B^ (trong một tam giác, góc đối diện với cạnh lớn hơn thì lớn hơn)

Chọn đáp án A.

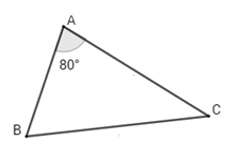
Bài 8: Cho ΔABC có ∠A = 80°, ∠B - ∠C = 20°. Chọn câu trả lời đúng nhất:

Lời giải:

Bài 9: Cho tam giác ABC có A^ = 3C^ và B^ = 5C^. Chọn khẳng định đúng trong các khẳng định sau:

A. AB < AC < BC

B. AC < AB < BC

C. AB < BC < AC

D. BC < AC < AB

Lời giải:

Chọn đáp án C

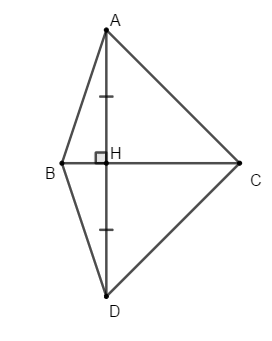
Bài 10: Cho tam giác ABC có C^ < B^ < 90°. Vẽ AH BC tại H, trên tia đối của tia HA lấy điểm D sao cho HA = HD. Câu nào sau đây sai?

A. AC > AB

B. DB > DC

C. DC > AB

D. AC > BD

Lời giải:

Chọn đáp án B

Bài 11: Cho tam giác ABC vuông tại A, tia phân giác góc B cắt AC tại

D. Khi so sánh độ dài của AD và DC, khẳng định nào sau đây đúng?

A. AD < DC

B. AD = DC

C. AD > DC

D. Không so sánh được

Lời giải:

Từ D kẻ đường thẳng vuông góc với BC cắt BC tại E

Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:

BD cạnh huyền chung

 (BD là tia phân giác của góc B)

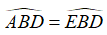
Khi đó: ΔABD = ΔEBD (cạnh huyền góc nhọn)

Suy ra: AD = DE (hai cạnh tương ứng) (1)

Lại có tam giác DEC vuông tại E có DC là cạnh huyền

Suy ra DC > DE (trong tam giác vuông, cạnh đối diện với góc vuông là cạnh lớn nhất) (2)

Từ (1) và (2) suy ra DC > AD hay AD < DC

Vậy A đúng, B, C, D sai.

Chọn đáp án A

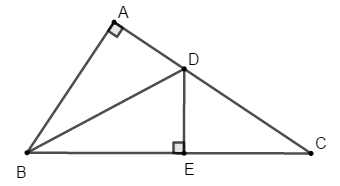
Bài 12: Cho tam giác ABC vuông tại A, có góc B không nhỏ hơn góc C và AD ⊥ BC tại D. Khi đó ta có:

A. AB < AC < AD

B. AB > AC > AD

C. AD < AB ≤AC

D. AD > AB ≥ AC

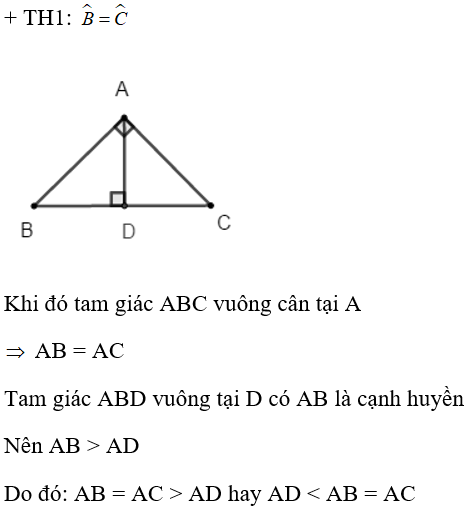
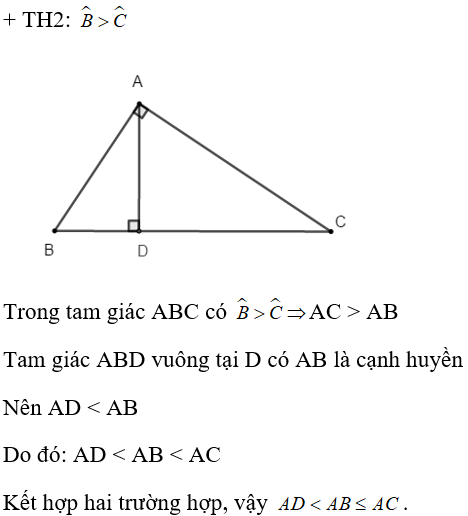
Lời giải:

Chọn đáp án C

Bài 12: Tam giác ABC có AB = 5 cm; BC = 6 cm và AC = 7 cm. Gọi A₁^; B₁^; C₁^ theo thứ tự là góc ngoài tại các đỉnh A, B, C của tam giác đó. Trong các khẳng định, khẳng định nào là đúng?

Lời giải:

Chọn đáp án B

Xem thêm các dạng bài tập hay, có đáp án:

60 Bài tập về Góc nhọn, góc tù, góc bẹt (có đáp án năm 2024)

50 Bài tập Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn (có đáp án năm 2024) - Toán 9

70 Bài tập về Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc (có đáp án năm 2024) - Toán 7

30 Bài tập Xác định góc giữa hai vectơ, góc giữa hai đường thẳng (2024) cực hay, chi tiết

65 Bài tập về Hai đường thẳng vuông góc. Hai đường thẳng song song (có đáp án năm 2024)