Bài giảng Toán 11 Bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian
Kiến thức cần nhớ
I. Phép chiếu song song
- Cho mặt phẳng (α) và đường thẳng ∆ cắt (α). Với mỗi điểm M trong không gian, đường thẳng đi qua M và song song hoặc trùng với ∆ sẽ cắt (α) tại điểm M’ xác định. Điểm M’ được gọi là hình chiếu song song của điểm M trên (α) theo phương ∆.
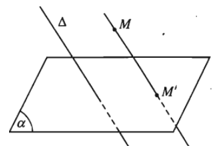
Mặt phẳng (α) gọi là mặt phẳng chiếu. Phương ∆ gọi là phương chiếu.
Phép đặt tương ứng mỗi điểm M trong không gian với hình chiếu M’ của nó trên (α) được gọi là phép chiếu song song lên (α) theo phương ∆.
Nếu H là một hình nào đó thì tập hợp H’ các hình chiếu M’ của tất cả những điểm M thuộc H được gọi là hình chiếu của H qua phép chiếu song song nói trên.
- Chú ý. Nếu một đường thẳng có phương trùng với phương chiếu thì hình chiếu của đường thẳng đó là một điểm.
II. Các tính chất của phép chiếu song song
- Định lí 1.
a) Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.
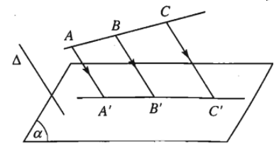
b) Phép chiếu song song biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng.
c) Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.
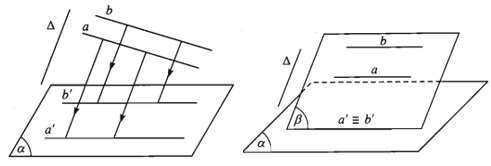
d) Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc cùng nằm trên một đường thẳng.
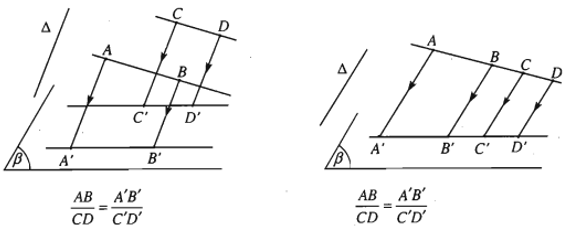
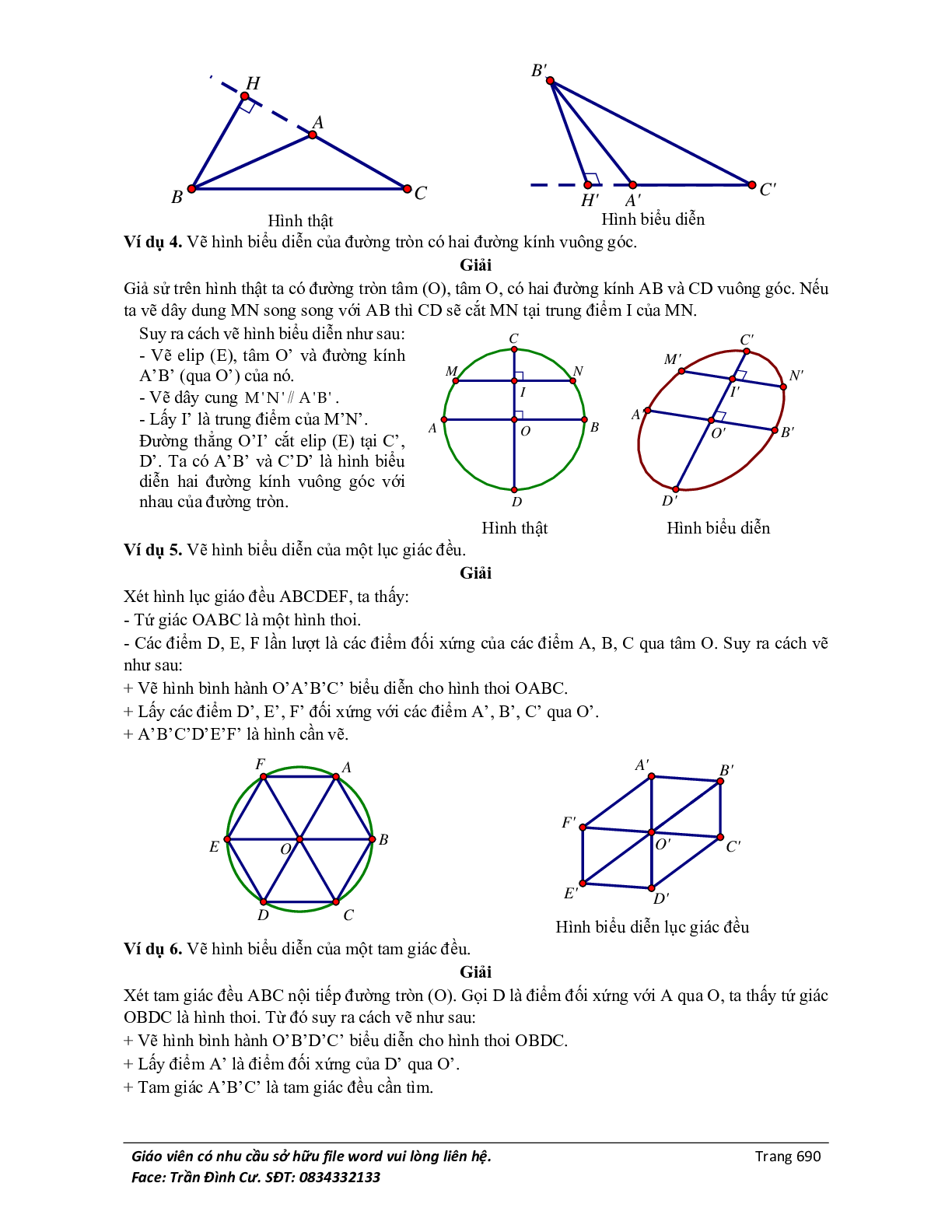
III. Hình biểu diễn của một hình không gian trên mặt phẳng.
Hình biểu diễn của hình H trong không gian là hình chiếu song song của hình H trên một mặt phẳng theo một phương chiếu nào đó hoặc hình đồng dạng với hình chiếu đó.
- Hình biểu diễn của các hình thường gặp.
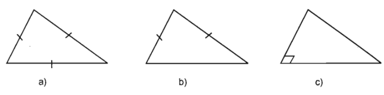
+ Tam giác: Một tam giác bất kì bao giờ cũng có thể coi là hình chiếu của một tam giác có dạng tùy ý cho trước (có thể là tam giác đều, tam giác cân, tam giác vuông, …).
+ Hình bình hành: Một hình bình hành bất kì bao giờ cũng có thể coi là hình biểu diễn của một hình bình hành tùy ý cho trước (có thể là hình bình hành, hình vuoongm hình thoi, hình chữ nhật, …).

+ Hình thang: Một hình thang bất kì bao giờ cũng có thể coi là hình biểu diễn của một hình thang tùy ý cho trước, miễn là tỉ số độ dài hai đáy của hình biểu diễn phải bằng tỉ số độ dài hai đáy của hình thang ban đầu.
+ Hình tròn: Người ta thường dùng hình elip để biểu diễn hình tròn.
Các dạng toán về Phép chiếu song song. Hình biểu diễn của một hình không gian
(Xem chi tiết trong file đính kèm)
Dạng 1. Vẽ hình biểu diễn của một hình trong không gian.
Dạng 2. Các bài toán liên quan đến phép chiếu song song.
Bài tập
1. Bài tập vận dụng (có đáp án)
I. Bài tập trắc nghiệm
Bài 1: Cho các đường thẳng không song song với phương chiếu. khẳng định nào sau đây là đúng?
A. phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song.
B. phép chiếu song song có thể biến hai đường thẳng song song thành hai đường thẳng cắt nhau.
C. phép chiếu song song có thể biến hai đường thẳng song song thành hai đường thẳng chéo nhau.
D. phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.
Lời giải:
Đáp án: D
Bài 2: Cho các đoạn thẳng không song song với phương chiếu. khẳng định nào sau đây là đúng?
A. phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng cùng nằm trên hai đường thẳng.
B. phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng khi và chỉ khi hai đoạn thẳng đó cùng nằm trên một đường thẳng.
C. phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng khi và chỉ khi hai đoạn thẳng đó cùng nằm trên hai đường thẳng song song.
D. phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng cùng nằm trên một đường thẳng hoặc nằm trên hai đường thẳng song song.
Lời giải:
Đáp án: D
Bài 3: Khẳng định nào sau đây là đúng?
A. hình biểu diễn một đường tròn là một đường tròn.
B. hình biểu diễn của một đường tròn có thể là nửa đường tròn.
C. hình biểu diễn của một đường tròn có thể là nửa đường eclip
D. hình biểu diễn của một đường tròn là một đường elip.
Lời giải:
Đáp án: D
Bài 4: Khẳng định nào sau đây là sai?
A. phép chiếu song song biến đường trung bình tam giác thành đường trung bình tam giác ảnh.
B. phép chiếu song song biến đường trung bình hình thang thành đường trung bình hình thang ảnh.
C. phép chiếu song song biến đường trung tuyến tam giác thành đường trung tuyến tam giác ảnh.
D. phép chiếu song song có thể biến đường trung tuyến tam giác thành đường thẳng không phải là trung tuyến tam giác ảnh.
Lời giải:
Đáp án: D
Bài 5: Hình biểu diễn của một hình thoi là hình nào sau đây?
A. hình thoi
B. hình bình hành
C. hình thang
D. hình tứ giác
Lời giải:
Đáp án: B
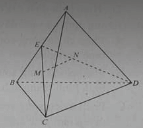
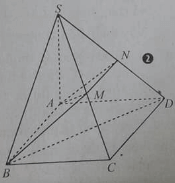
Bài 6: Cho hình chóp S.ABCD có đáy là hình bình hành. M là trung điểm của SC. Hình chiếu song song của điểm M theo phương AB lên mặt phẳng (SAD) là điểm nào sau đây?
A. S
B. trung điểm của SD
C. A
D. D
Lời giải:
Đáp án: B
(hình 2) Do (MAB) chứa AB//CD, nên giao tuyến của (MAB) với (SCD) là đường thẳng đi qua M và song song với AB. Đường thẳng này cắt SD tại điểm N. khi đó MN là đường trung bình của tam giác SCD nên N là trung điểm của SD.
Bài 7: Khẳng định nào sau đây là đúng.
A. Hình biểu diễn của một hình bình hành là một hình bình hành.
B. Hình biểu diễn của một hình chữ nhật là một hình chữ nhật.
C. Hình biểu diễn của một hình vuông là một hình vuông.
D. Hình biểu diễn của một hình thoi là một hình thoi.
Lời giải:
Đáp án: A
Các phương án B, C sai vì phép chiếu song song không bảo toàn góc. Phương án D sau vì phép chiếu song song chưa chắc bảo toàn tỉ số hai đoạn nằm trên hai đường thẳng cắt nhau. Đáp án A
Bài 8: Khẳng định nào sau đây là sai?
A. Phép chiếu song song biến trung điểm của đoạn thẳng thành trung điểm của đoạn thẳng hình chiếu.
B. Phép chiếu song song biến trọng tâm tam giác thành trọng tâm tam giác hình chiếu.
C. Phép chiếu song song biến tam của hình bình hành thành tâm của hình bình hành.
D. Phép chiếu song song có thể biến trọng tâm tam giác thành một điểm không phải là trọng tâm tam giác hình chiếu.
Lời giải:
Đáp án: D
Phương án D sai vì phép chiếu song song bảo toàn tỉ lệ các đoạn thẳng cùng nằm trên một đoạn thẳng. Đáp án D.
Bài 9: Hình biểu diễn của một tam giác đều là hình nào sau đây?
A. Tam giác đều
B. Tam giác cân
C. Tam giác vuông
D. Tam giác
Lời giải:
Đáp án: D
Bài 10: Cho tứ diện ABCD. M là trọng tâm của tam giác ABC. Hình chiếu song song của điểm M theo phương CD lên mặt phẳng (ABD) là điểm nào sau đây?
A. Điểm A
B. Điểm B
C. Trọng tâm tam giác ABD
D. Trung điểm của đường trung tuyến ket từ D của tam giác ABD
Lời giải:
Đáp án: C
Gọi E là trung điểm của AB.M, N lần lượt là trọng tâm của tam giác ABC, ABD nên:
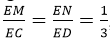
Theo định lí Ta-lét ta có MN // CD. Vậy hình chiếu song song của điểm M theo phương CD lên mặt phẳng (ABD) là trọng tâm của tam giác ABD. Đáp án C.
II. Bài tập tự luận có lời giải
Bài 1 Hình chiếu song song của một hình vuông có thể là hình bình hành được không?
Lời giải
Hình chiếu song song của một hình vuông có thể là hình bình hành
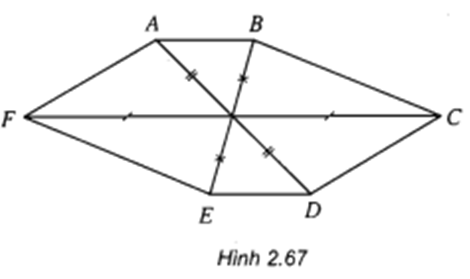
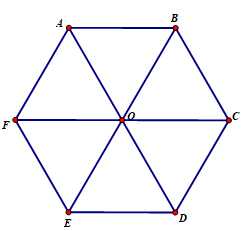
Bài 2 Hình 2.67 có thế là hình chiếu song song của hình lục giác đều được không? Vì sao?
Lời giải
Hình 2.67 không thể là hình chiếu song song của hình lục giác đều vì
Lục giác đều ABCDEF có O là giao điểm các đường chéo
Ta có: AO // BC
Trên hình 2.67 không biểu diễn được điều đó
(Phép chiếu song song biến hai đường thằng song song thành hai đường thẳng song song hoặc trùng nhau)
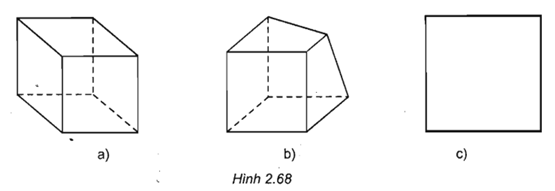
Bài 3 Trong các hình 2.68, hình nào biểu diễn cho hình lập phương?
Lời giải
Hình a biểu diễn hình lập phương
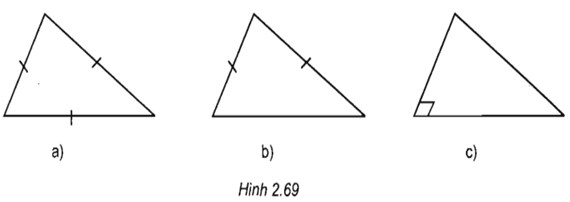
Bài 4 Các hình 2.69a, 2.69c, 2.69c là hình biểu diễn của tam giác nào?
Lời giải
Hình 2.69a là hình biểu diễn của tam giác đều
Hình 2.69b là hình biểu diễn của tam giác cân
Hình 2.69c là hình biểu diễn của tam giác vuông
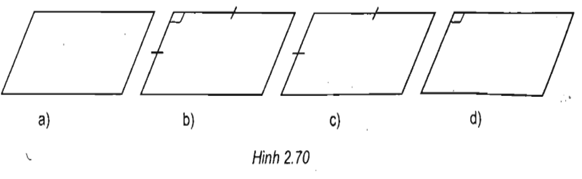
Bài 5 Các hình 2.70a, 2.70b, 2.70c, 2.70d là hình biểu diễn của các hình bình hành nào (hình bình hành, hình thoi, hình vuông, hình chữ nhật)?
Lời giải
Hình 2.70a biểu diễn hình bình hành
Hình 2.70b biểu diễn hình vuông
Hình 2.70c biểu diễn hình thoi
Hình 2.70d biểu diễn hình chữ nhật
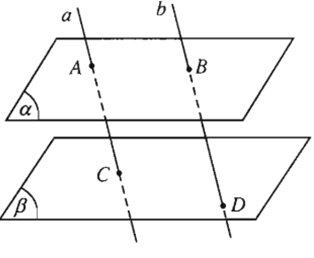
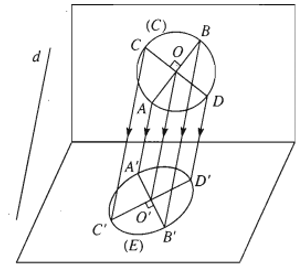
Bài 6 Cho hai mặt phẳng (α) và (β) song song với nhau. Đường thẳng a cắt (α) và (β) lần lượt tại A và C. Đường thẳng b song song với a cắt (α) và (β) lần lượt tại B và D.
Hình 2.72 minh họa nội dung trên đúng hay sai?
Lời giải
Sai vì
Ta có định lí 3 trang 67: cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song
Theo đề bài ta có: (α) // (β)
a//b nên A,B,C,D thuộc mặt phẳng
AB là giao tuyến của (α) và (ABDC)
CD là giao tuyến của (β) và (ABDC)
⇒ AB // CD (theo định lí)
Hình 2.72 không biểu diễn được AB // CD
2. Bài tập tự luyện có hướng dẫn
(Xem trong file đính kèm)
Xem thêm các dạng bài tập toán hay khác:
90 Bài tập về hai mặt phẳng vuông góc (có đáp án năm 2024)
100 Bài tập về đường thẳng vuông góc với mặt phẳng (có đáp án năm 2024)
70 Bài tập về hai đường thẳng vuông góc (có đáp án năm 2024)
70 Bài tập về vectơ trong không gian (có đáp án năm 2024)