Bài giảng Toán 11 Bài 2: Hai đường thẳng vuông góc
Kiến thức cần nhớ
1. Tích vô hướng của hai vecto trong không gian
1.1. Góc giữa hai vecto trong không gian
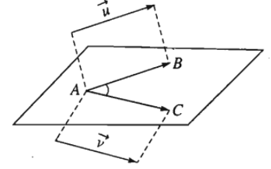
- Định nghĩa. Trong không gian, cho →u ; →v là hai vecto khác vecto- không. Lấy một điểm A bất kì, gọi B và C là hai điểm sao cho →AB = →u ; →AC = →v. Khi đó, ta gọi góc ^BAC (00 ≤^BAC ≤1800) là góc giữa hai vecto →u ; →v trong không gian.
Kí hiệu là (→u ; →v).
1.2. Tích vô hướng của hai vecto trong không gian
- Định nghĩa:
Trong không gian có hai vecto →u ; →v đều khác vecto- không . Tích vô hướng của hai vecto là một số, kí hiệu là →u ; →v, được xác định bởi công thức: →u . →v = |→u|. |→v|.cos (→u; →v)
Trường hợp →u= →0 hoặc →v= →0 ta quy ước: →u . →v = 0.
Ví dụ 1. Cho hình chóp S.ABC có SA= SB= SC và ^ASB = ^BSC = ^CSA. Hãy xác định góc giữa cặp vectơ →SC và →AB?
Lời giải :
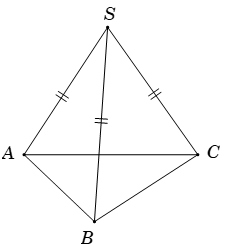
Ta có
→SC.→AB=→SC.(→SB−→SA)=→SC.→SB−→SC.→SA=|→SC|.|→SB|.cos(→SC.→SB)− |→SC|.|→SA|.cos(→SC.→SA)=SC.SB.cos^BSC− SC.SA.cos^ASC
Vì SA= SB= SC và ^ASB = ^BSC = ^CSA⇒→SC.→AB=0
Ta lại có:
→SC.→SA=|→SC|.|→SA|.cos(→SC,→SA)⇒cos(→SC,→SA)=0
Do đó (→SC; →AB) =900.
2. Vector chỉ phương của đường thẳng
2.1. Định nghĩa
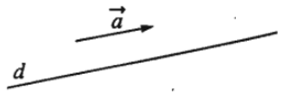
Nếu →a khác vecto - không được gọi là vecto chỉ phương của đường thẳng d nếu giá của vecto →a song song hoặc trùng với đường thẳng d.
2.2. Nhận xét
a) Nếu →a là vecto chỉ phương của đường thẳng d thì vecto k→a (k ≠0) cũng là vecto chỉ phương của d.
b) Một đường thẳng d trong không gian hoàn toàn được xác định nếu biết một điểm A thuộc đường thẳng d và một vecto chỉ phương của nó.
c) Hai đường thẳng song song với nhau khi và chỉ khi chúng là hai đường thẳng phân biệt và có hai vecto chỉ phương cùng phương.
3. Góc giữa hai đường thẳng trong không gian
3.1. Định nghĩa
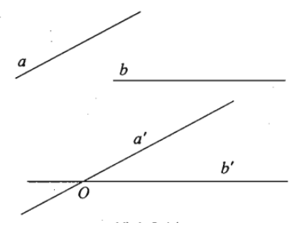
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm và lần lượt song song với a và b.
3.2. Nhận xét
a) Để xác định góc giữa hai đường thẳng a và b ta có thể lấy điểm O thuộc một trong hai đường thẳng đó rồi vẽ một đường thẳng qua O và song song với đường thẳng còn lại.
b) Nếu →u là vecto chỉ phương của đường thẳng a và là →v vecto chỉ phương của đường thẳng b và (→u; →v) = α thì góc giữa hai đường thẳng a và b bằng nếu 00≤α≤900 và bằng 1800− α nếu 900< α≤1800.
Nếu a và b song song hoặc trùng nhau thì góc giữa chúng bằng 00.
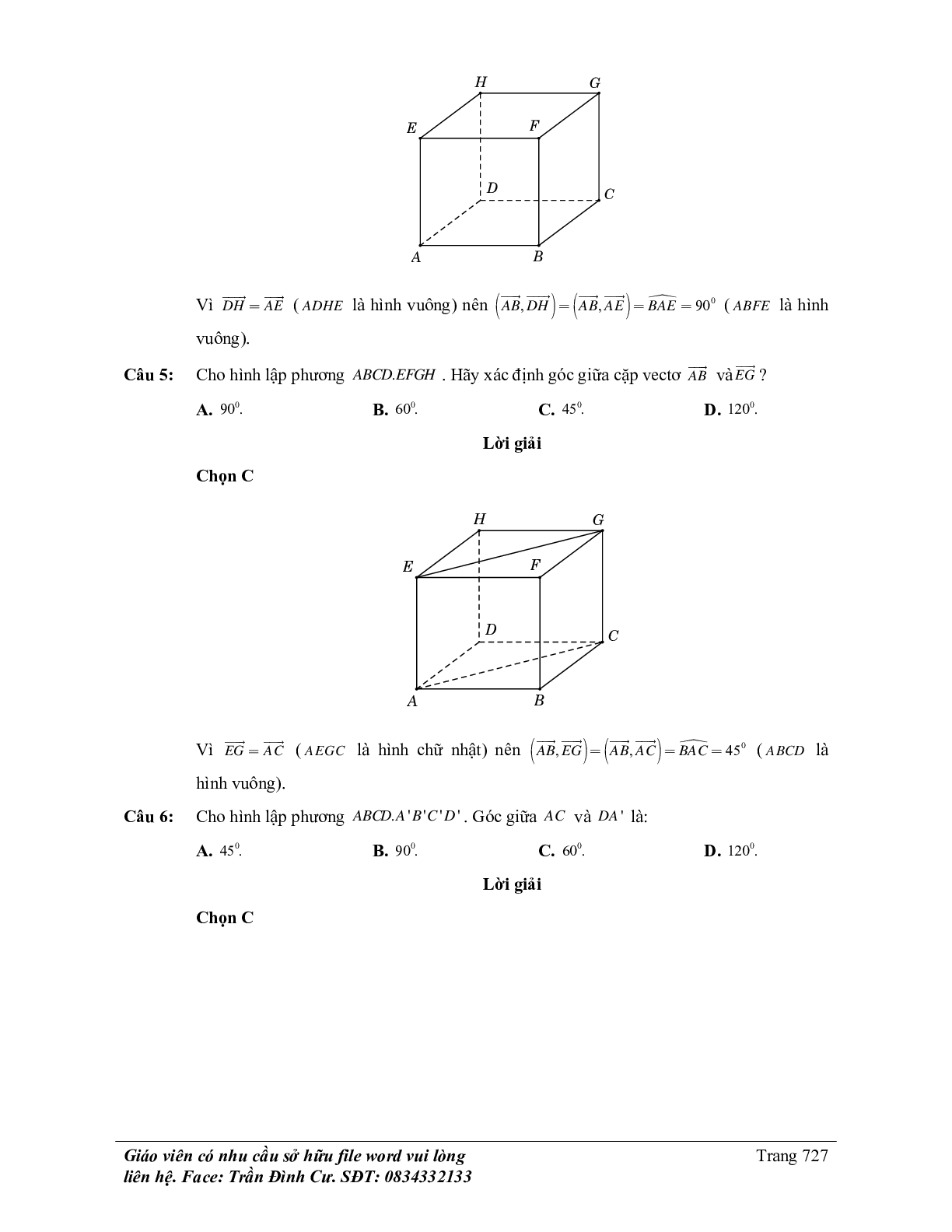
Ví dụ 2. Cho hình lập phương ABCD.A’B’C’D’. Tính góc giữa AC và DA’
Lời giải:
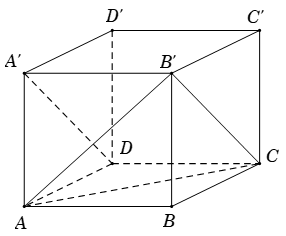
Gọi a là độ dài cạnh hình lập phương.
Khi đó, tam giác AB’C đều (AB’ = B’C= CA = a√2)
Do đó ^B'CA =600.
Lại có, DA’ song song CB’ nên
(AC ; DA’) = (AC ; CB’) = ^B'CA =600.
4. Hai đường thẳng vuông góc
4.1. Định nghĩa
Hai đường thẳng được gọi là vuông góc nếu góc giữa chúng bằng 900.
Ta kí hiệu hai đường thẳng a và b vuông góc với nhau là a ⊥ b.
4.2. Nhận xét
a) Nếu →u; →v lần lượt là các vecto chỉ phương của hai đường thẳng a và b thì a ⊥ b⇔→u. →v =0.
b) Cho hai đường thẳng song song. Nếu một đường thẳng vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
c) Hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhau.
Ví dụ 3. Cho tứ diện ABCD có AB= AC= AD và ^BAC = ^BAD =600; ^CAD = 900. Gọi I và J lần lượt là trung điểm của AB và CD. Chứng minh hai đường thẳng AB và IJ vuông góc với nhau.
Lời giải:
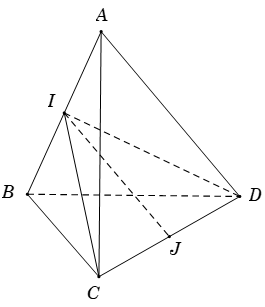
Xét tam giác ICD có J là trung điểm đoạn CD ⇒→IJ=12(→IC+→ID).
Tam giác ABC có AB = AC và ^BAC =600 nên tam giác ABC đều
⇒CI ⊥AB. (1)
Tương tự, ta có tam giác ABD đều nên DI ⊥AB. ( 2)
Từ (1) và (2) ta có :
→IJ.→AB=12(→IC+→ID).→AB =12→IC.→AB+12→ID.→AB=0⇒→IJ ⊥→AB ⇒IJ⊥AB
Các dạng toán về hai đường thẳng vuông góc
Dạng 1. Tính góc giữa hai đường thẳng.
Dạng 2. Chứng minh hai đường thẳng vuông góc trong không gian.
Bài tập có hướng dẫn
1. Bài tập vận dụng
Bài 1. Cho tứ diện ABCD có BA = CD. Gọi I ; J ; E ; F lần lượt là trung điểm của AC ; BC ; BD ; AD. Tính góc ( IE ; JF)
Lời giải :
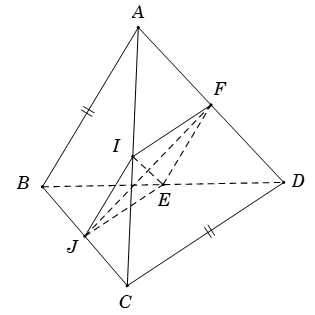
Ta có IF là đường trung bình của tam giác ACD ⇒{IF ∥ CDIF=12CD ( 1)
Lại có JE là đường trung bình của tam giác BCD ⇒{JE ∥ CDJE=12CD ( 2)
Từ (1) và (2) suy ra : IF = JE và IF// JE.
Suy ra, tứ giác IJEF là hình bình hành.
Mặt khác: {IJ=12ABJE=12CD. Mà AB= CD nên IJ= JE.
Do đó IJEF là hình thoi.
Suy ra ( IE ; JF) = 900.
Bài 2. Cho tứ diện ABCD có AB = CD = a, IJ=a√32 ( I; J lần lượt là trung điểm của BC và AD). Tính số đo góc giữa hai đường thẳng AB và CD:
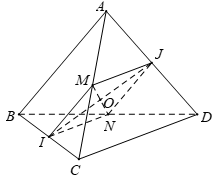
Gọi M; N lần lượt là trung điểm AC; BD.
Ta có:
{MI=NI=12AB=12CD=a2MI // AB // CD // NI ⇒MINJ là hình thoi.
Gọi O là giao điểm của MN và IJ.
Ta có: ^MIN=2^MIO.
Xét tam giác MIO vuông tại O, ta có:
cos^MIO=IOMI=a√34a2=√32⇒^MIO=30°⇒^MIN=60°
Mà: (AB,CD)=(IM,IN)=^MIN=60°
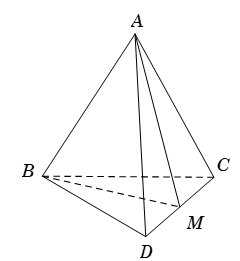
Bài 3. Cho tứ diện đều ABCD. Số đo góc giữa hai đường thẳng AB và CD bằng:
Lời giải :
Gọi M là trung điểm của CD.
Tam giác ACD và tam giác BCD là tam giác đều ( vì ABCD là tứ diện đều) có AM ; BM là hai đường trung tuyến ứng với cạnh CD nên đồng thời là đường cao. ⇒→CD. →AM =0; →CD. →MB =0;
Do đó →CD.→AB=→CD.(→AM+→MB) =→CD.→AM+→CD.→MB=0.
Suy ra →AB ⊥→CD nên số đo góc giữa hai đường thẳng AB và CD bằng 900
2. Bài tập tự luyện có hướng dẫn
(Xem thêm các bài tập trong file pdf)
Xem thêm các dạng bài tập liên quan khác:
100 Bài tập về đường thẳng vuông góc với mặt phẳng (có đáp án năm 2023)
90 Bài tập về hai mặt phẳng vuông góc (có đáp án năm 2023)