Bài giảng Toán 11 Bài 1: Giới hạn của dãy số
Kiến thức cần nhớ
a) Dãy số có giới hạn 0
Ta nói rằng dãy số (un) có giới hạn là 0 khi n dần tới dương vô cực, nếu với mỗi số dương nhỏ tùy ý cho trước, mọi số hạng của dãy số kể từ một số hạng nào đó trở đi, |un| nhỏ hơn số dương đó.
Kí hiệu: limn→∞un=0 hay lim un = 0 hay un→0 khi n→+∞.
b) Dãy số có giới hạn hữu hạn
Ta nói rằng dãy số (un) có giới hạn là số thực L nếu lim (un – L) = 0
Kí hiệu: limn→∞un=L hay lim un = L hay un→L khi n→+∞.
c) Dãy số có giới hạn vô cực
Dãy số (un) có giới hạn là +∞ khi n→+∞, nếu un có thể lớn hơn một số dương bất kì kể từ một số hạng nào đó trở đi.
Ký hiệu: limun=+∞ hoặc un→+∞
Dãy số (un) có giới hạn là khi , nếu
Ký hiệu: hoặc
d) Một vài giới hạn đặc biệt
e) Định lý về giới hạn hữu hạn
* Nếu lim un = a và lim vn = b và c là hằng số. Khi đó ta có :
lim(un + vn) = a + b
lim(un - vn) = a - b
lim(un vn) = a.b
lim(cun ) = c.a
lim|un | = |a|
Nếu với mọi n thì và .
* Định lí kẹp: Cho ba dãy số (vn); (un) và (wn):
Nếu thì lim un = a.
Hệ quả: Cho hai dãy số (un) và (vn):
Nếu thì lim un = 0.
f) Một vài quy tắc tìm giới hạn vô cực
* Quy tắc tìm giới hạn tích lim (unvn)
Nếu . Khi đó: lim (unvn)
|
lim un = L |
lim vn |
lim (unvn) |
|
+ |
||
|
+ |
||
|
- |
||
|
- |
* Quy tắc tìm giới hạn thương
|
lim un = L |
lim vn |
Dấu của vn |
|
|
L |
Tùy ý |
0 |
|
|
L > 0 |
0 |
+ |
|
|
0 |
- |
||
|
L < 0 |
0 |
+ |
|
|
0 |
- |
g) Tổng cấp số nhân lùi vô hạn
Xét cấp số nhân vô hạn u1; u1q; u1q2; … u1qn; … có công bội |q| < 1 được gọi là cấp số nhân lùi vô hạn.
Tổng của cấp số nhân lùi vô hạn là:
Các dạng toán về giới hạn của dãy số
Dạng 1: Tính giới hạn sử dụng một vài giới hạn đặc biệt
Phương pháp giải:
Sử dụng các giới hạn đặc biệt:
Ví dụ minh họa:
Ví dụ 1: Tính các giới hạn sau:
a)
b)
c)
Lời giải
Áp dụng công thức tính giới hạn đặc biệt, ta có:
a)
b)
c)
Ví dụ 2: Tính các giới hạn sau:
a)
b)
c) lim (-0,999)n
Lời giải
a) vì
b) vì
c) lim (-0,999)n = 0 vì |-0,999| < 1.
Dạng 2: Tính giới hạn hữu hạn của phân thức
Phương pháp giải:
Trường hợp lũy thừa của n: Chia cả tử và và mẫu cho nk (với nk là lũy thừa với số mũ lớn nhất).
Trường hợp lũy thừa mũ n: Chia cả tử và mẫu cho lũy thừa có cơ số lớn nhất.
Sử dụng một vài giới hạn đặc biệt:
Ví dụ minh họa:
Ví dụ 1: Tính các giới hạn sau
a)
b)
c)
Lời giải
a)
Vì và .
b)
Vì
c)
Vì
Ví dụ 2: Tính các giới hạn sau:
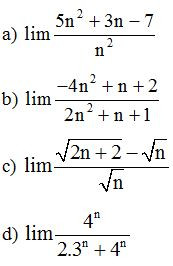
Lời giải
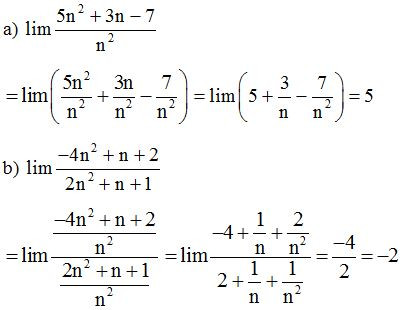
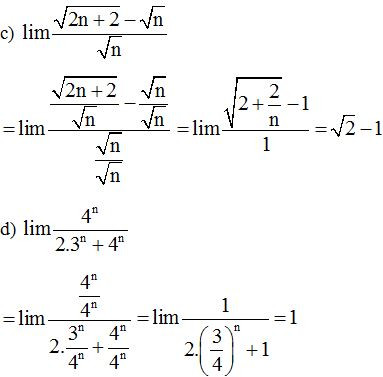
Dạng 3: Tính giới hạn hữu hạn sử dụng phương pháp liên hợp
Phương pháp giải:
Sử dụng các công thức liên hợp (thường sử dụng trong các bài toán chứa căn)
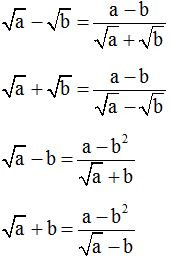
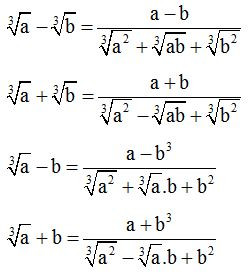
Ví dụ minh họa:
Ví dụ 1: Tính các giới hạn sau:
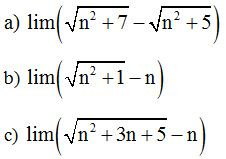
Lời giải
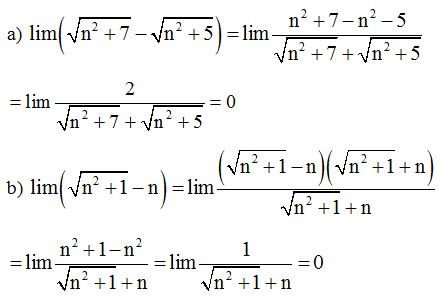

Ví dụ 2: Tính giới hạn sau:
Lời giải
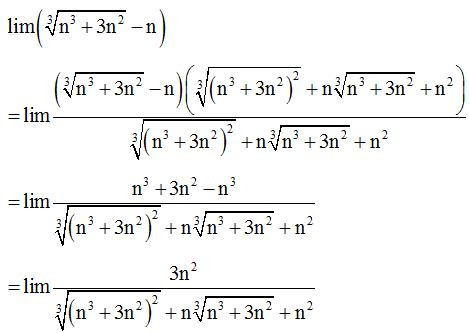

Dạng 4: Tính giới hạn ra vô cực dạng chứa đa thức hoặc căn thức
Phương pháp giải:
Rút bậc lớn nhất của đa thức làm nhân tử chung.
Sử dụng quy tắc giới hạn tới vô cực lim (unvn)
Nếu . Khi đó: lim (unvn)
|
lim un = L |
lim vn |
lim (unvn) |
|
+ |
||
|
+ |
||
|
- |
||
|
- |
Ví dụ minh họa:
Ví dụ 1: Tính các giới hạn sau:
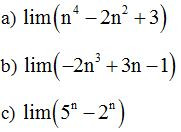
Lời giải
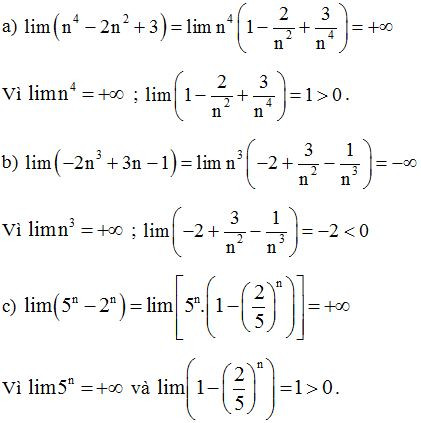
Ví dụ 2: Tính các giới hạn sau
a)
b)
Lời giải
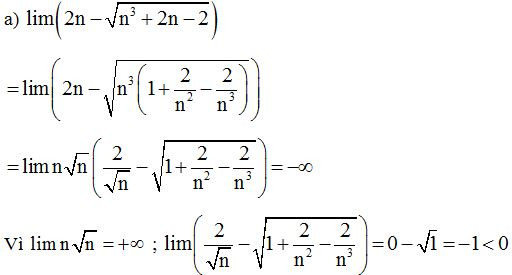
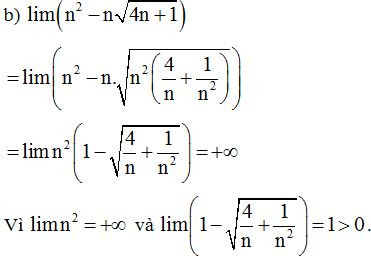
Dạng 5: Tính giới hạn ra vô cực dạng phân thức
Phương pháp giải:
Rút bậc lớn nhất của tử và mẫu ra làm nhân tử chung.
Sử dụng quy tắc giới hạn tới vô cực lim (unvn)
Nếu . Khi đó: lim (unvn)
|
lim un = L |
lim vn |
lim (unvn) |
|
+ |
+ | + |
|
+ |
- | - |
|
- |
+ | - |
|
- |
- | + |
Ví dụ minh họa:
Ví dụ 1: Tính các giới hạn sau:
a)
b)
Lời giải
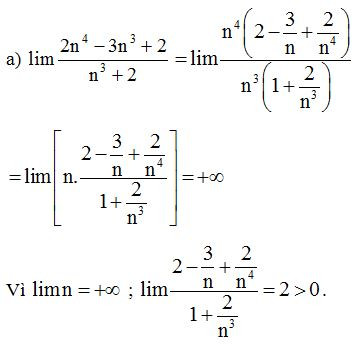
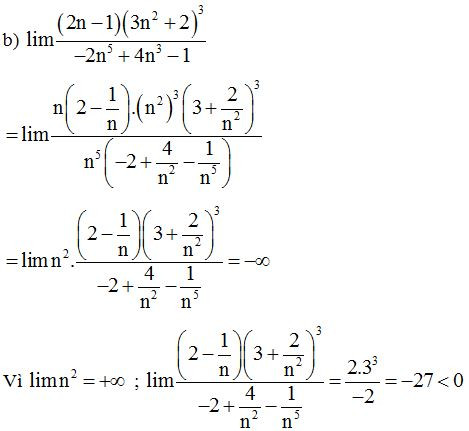
Ví dụ 2: Tính giới hạn sau .
Lời giải
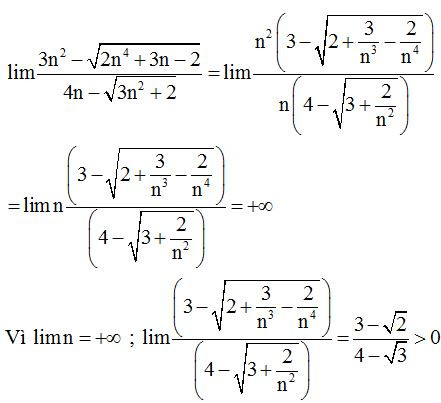
Dạng 6: Tính giới hạn sử dụng định lý kẹp
Phương pháp giải:
Sử dụng định lý kẹp và hệ quả của định lý kẹp
Định lí kẹp: Cho ba dãy số (vn); (un) và (wn): Nếu thì lim un = a
Hệ quả: Cho hai dãy số (un) và (vn): Nếu thì lim un = 0.
Ví dụ minh họa:
Ví dụ 1: Tính các giới hạn sau:
a)
b)
Lời giải
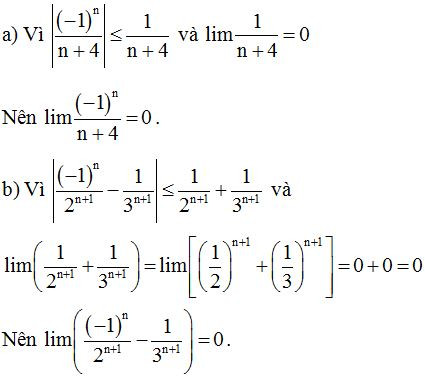
Ví dụ 2: Tính các giới hạn sau :
a)
b)
Lời giải
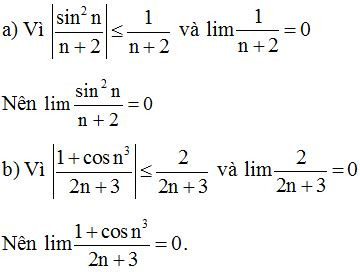
Dạng 7: Giới hạn dãy số có công thức truy hồi
Phương pháp giải:
Cho dãy số (un) ở dạng công thức truy hồi, biết (un) có giới hạn hữu hạn
Giả sử lim un = a (a là số thực) thì lim un+1 = a.
Thay a vào công thức truy hồi. Giải phương trình tìm a.
Ta được giới hạn của (un) là lim un = a.
Ví dụ minh họa:
Ví dụ 1: Tìm lim un biết (un) có giới hạn hữu hạn và
Lời giải
Giả sử lim un = a, khi đó lim un+1 = a
Suy ra
Do nên
Vậy .
Ví dụ 2: Tìm lim un biết (un) có giới hạn hữu hạn và .
Lời giải
Vì
Giả sử lim un = a (a > 0), khi đó lim un+1 = a
Suy ra
Vậy lim un = 2.
Dạng 8: Giới hạn của tổng vô hạn hoặc tích vô hạn
Phương pháp giải:
* Rút gọn (un) (sử dụng tổng cấp số cộng, cấp số nhân hoặc phương pháp làm trội)
* Rồi tìm lim un theo định lí hoặc dùng nguyên lí định lí kẹp.
* Định lí kẹp: Cho ba dãy số (vn); (un) và (wn): Nếu thì lim un = a
Hệ quả: Cho hai dãy số (un) và (vn): Nếu thì lim un = 0.
Ví dụ minh họa:
Ví dụ 1: Tính các giới hạn sau:
a)
b)
Lời giải
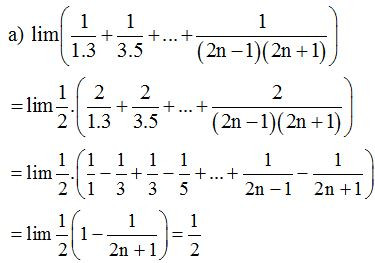
b)
Xét tử số: Ta thấy 1; 2; 3; 4; … ; n là một dãy số thuộc cấp số cộng có n số hạng với u1 = 1 và d = 1.
Tổng n số hạng của cấp số cộng:
Xét mẫu số: Ta thấy 1; 3 ; 32 ; 33 ; … ; 3n là một dãy số thuộc cấp số nhân có (n+1) số hạng với u1 = 1 và q = 3.
Tổng (n + 1) số hạng của cấp số nhân:
Khi đó:
Vì và
Nên
(Bằng quy nạp ta luôn có và ).
Ví dụ 2: Tính giới hạn sau:
Lời giải
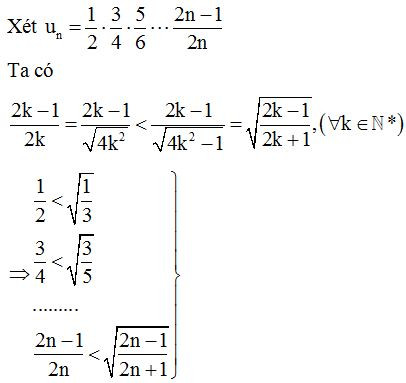
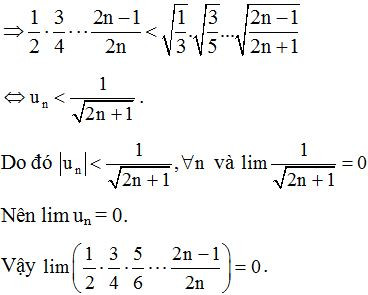
Dạng 9: Tổng cấp số nhân lùi vô hạn
Phương pháp giải:
Tổng của cấp số nhân lùi vô hạn là:
Ví dụ minh họa:
Ví dụ 1: Tính tổng
a)
b)
Lời giải
a) là tổng cấp số nhân lùi vô hạn với u1 = 1 và .
Nên .
b) là cấp số nhân lùi vô hạn với u1 = 1 và q = 0,9.
Nên .
Ví dụ 2: Biểu diễn các số thập phân vô hạn tuần hoàn ra phân số:
a) a = 0,32111...
b) b = 2,151515...
Lời giải
a) Ta có
Vì là tổng của cấp số nhân lùi vô hạn với và
Nên .
b) Ta có
Vì là tổng của cấp số nhân lùi vô hạn với và
Nên .
Bài tập tự luyện
1. Bài tập vận dụng
Câu 1. Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
A. .
B. .
C. .
D. .
Câu 2. Dãy số nào sau đây có giới hạn bằng 0?
A. .
B. .
C. .
D. .
Câu 3. Dãy số nào sau đây có giới hạn bằng 0?
A. .
B. .
C. .
D. .
Câu 4. Tính giới hạn bằng
A. 0.
B. 1.
C. .
D. 2.
Câu 5. Cho dãy số (un) với . Khi đó lim un bằng
A. .
B. 0.
C. .
D. 1.
Câu 6. Cho dãy số (un) với . Khi đó lim un bằng
A. 2.
B. 1.
C. .
D. Không có giới hạn.
Câu 7. Tính bằng:
A. .
B. .
C. -1.
D. 0.
Câu 8. Tính bằng:
A. .
B. .
C. .
D. -4.
Câu 9. Tính bằng:
A. .
B. .
C. .
D. .
Câu 10. Trong bốn giới hạn sau đây, giới hạn nào là 0?
A. .
B. .
C. .
D. .
Câu 11. Cho dãy số (un) được xác định bởi với mọi . Biết dãy số (un) có giới hạn hữu hạn, lim un bằng:
A. -1.
B. 2.
C. 4.
D. .
Câu 12. Giới hạn dãy số (un) với là
A. .
B. .
C. .
D. 0.
Câu 13. Chọn kết quả đúng của .
A. 5.
B. .
C. .
D. .
Câu 14. Tổng bằng:
A. 1.
B. .
C. .
D. .
Câu 15. Biểu diễn số thập phân 1,24545454545… như một phân số:
A. .
B. .
C. .
D. .
Bảng đáp án
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
C |
D |
D |
A |
A |
B |
B |
C |
D |
D |
B |
A |
D |
B |
B |
2. Bài tập tự luyện có hướng dẫn
(Xem trong file đính kèm bên dưới)
Xem thêm các dạng bài tập liên quan khác:
70 Bài tập về hàm số liên tục (2024) có đáp án hay nhất
500 Bài tập Toán 11 chương 4: Giới hạn (có đáp án năm 2023)
70 Bài tập về giới hạn của dãy số (có đáp án năm 2023)
300 Bài tập Toán 11 chương 3: Dãy số - Cấp số cộng và cấp số nhân (có đáp án năm 2023)