Bài giảng Toán 8 Bài 1: Liên hệ giữa thứ tự và phép cộng
Kiến thức cần nhớ
1. Thứ tự trên tập hợp số
Trên tập hợp số thực, khi so sánh hai số a và b, có thể xảy ra một trong ba trường hợp sau:
Số a bằng số b, kí hiệu a = b;
Số a nhỏ hơn số b, kí hiệu a < b;
Số a lớn hơn số b, kí hiệu a > b.
Ví dụ 1.
3-2=-1812;
−25,08 < −22,5;
2,45 > 1,75.
Khi biểu diễn số thực trên trục số (vẽ theo phương nằm ngang), điểm biểu diễn số nhỏ hơn ở bên trái điểm biểu diễn số lớn hơn.
Ví dụ 2. Biểu diễn các số −0,75 và trên trục số như sau:
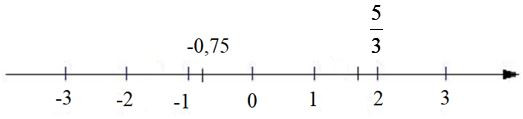
Ta thấy: trên trục số, điểm biểu diễn số −0,75 nằm bên trái điểm biểu diễn số 53.
Do đó −0,75 < 53.
2. Bất đẳng thức
Hệ thức dạng a < b (hay dạng a > b; a ≥ b; a ≤ b) được gọi là bất đẳng thức và gọi a là vế trái, b gọi là vế phải của bất đẳng thức.
Ví dụ 3. Bất đẳng thức (−3) + 5 > −4 có vế trái là (−3) + 5 và vế phải là (−4).
3. Liên hệ giữa thứ tự và phép cộng
a) Tính chất
Khi cộng cùng một số vào cả hai vế của một bất đẳng thức ta được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.
b) Tổng quát
Cho ba số a, b và c, ta có:
Nếu a < b thì a + c < b + c;
Nếu a ≤ b thì a + c ≤ b + c;
Nếu a > b thì a + c > b + c;
Nếu a ≥ b thì a + c ≥ b + c.
Ví dụ 4. Chứng minh 2021 + (−32) < 2022 + (−32).
Lời giải:
Theo tính chất trên, cộng (−32) vào hai vế của bất đẳng thức 2021 < 2022.
Ta suy ra 2021 + (−32) < 2022 + (−32).
Bài tập (có đáp án)
1. Bài tập vận dụng
Bài 1. Mỗi khẳng định sau đúng hay sai? Vì sao?
a) −5 > 3 + (−10);
b) 2 . (−6) < 2 . (−8);
c) −6 ≤ 2 . (−4);
d) x2 + 2 ≥ 2.
Lời giải:
a) Ta có: 3 + (−10) = −7.
Vì −5 > −7 nên −5 > 3 + (−10).
Do đó khẳng định −5 > 3 + (−10) là đúng.
b) Ta có: 2 . (−6) = −12; 2 . (−8) = − 16.
Vì −12 > −16 nên 2 . (−6) > 2 . (−8).
Do đó khẳng định 2 . (−6) < 2 . (−8) là sai.
c) Ta có: 2 . (−4) = −8.
Vì −6 > −8 nên −6 > 2 . (−4)
Do đó khẳng định −6 ≤ 2 . (−4) là sai.
d) Với mọi số thực x ta có: x2 ≥ 0.
Suy ra x2 + 2 ≥ 2.
Do đó khẳng định x2 + 2 ≥ 2 đúng với mọi số thực x.
Vậy khẳng định a) và d) là đúng, khẳng định b) và c) là sai.
Bài 2. Cho a > b, hãy so sánh:
a) a + 25 và b + 25;
b) a – 12 và b – 12.
Lời giải:
Ta có bất đẳng thức: a > b.
a) Cộng cả hai vế của bất đẳng thức a > b với 25, ta được:
a + 25 > b + 25.
b) Cộng cả hai vế của bất đẳng thức a > b với (–12), ta được:
a + (–12) < b + (–12)
Vậy a – 12 < b – 12.
Bài 3. So sánh a và b nếu:
a) a – 34 ≤ b – 34;
b) 21 + a ≥ 21 + b.
Lời giải:
a) Ta có: a – 34 ≤ b – 34.
Cộng hai vế của bất đẳng thức a – 34 ≤ b – 34 với 34, ta được:
a – 34 + 34 ≤ b – 34 + 34.
Do đó a ≤ b.
b) Ta có: 21 + a ≥ 21 + b.
Cộng hai vế của bất đẳng thức 21 + a ≥ 21 + b với (−21), ta được:
21 + a + (−21) ≥ 21 + b + (−21).
Do đó a ≥ b.
2. Bài tập tự luyện có hướng dẫn
Xem thêm các dạng Toán hay, chọn lọc khác :
60 Bài tập về Tính chất cơ bản của phân thức (có đáp án năm 2023)
60 Bài tập về Rút gọn phân thức (có đáp án năm 2023)
60 Bài tập về Quy đồng mẫu thức nhiều phân thức (có đáp án năm 2023)
60 Bài tập phép cộng các phân thức đại số (có đáp án năm 2023)
60 Bài tập về phép trừ các phân thức đại số (có đáp án năm 2023)









