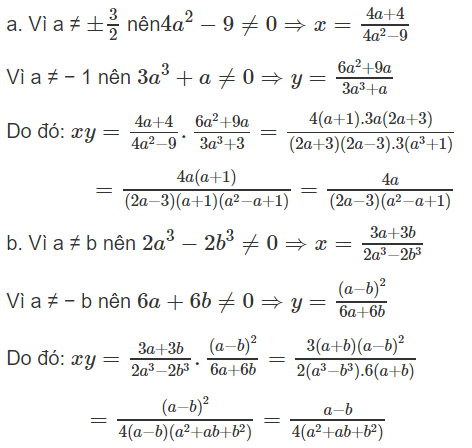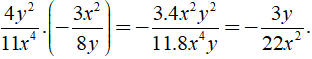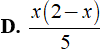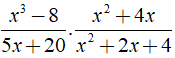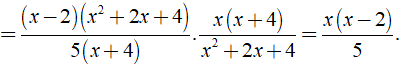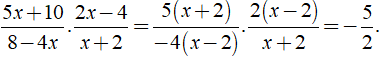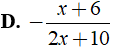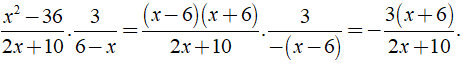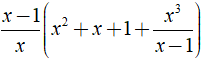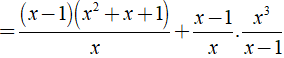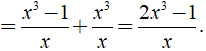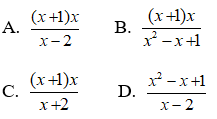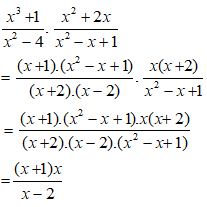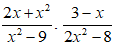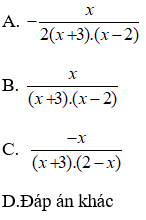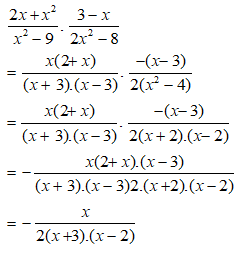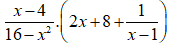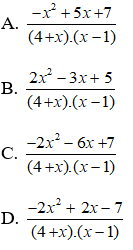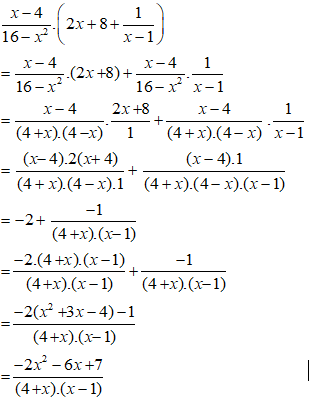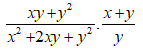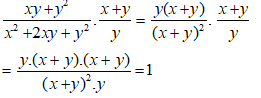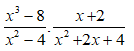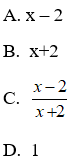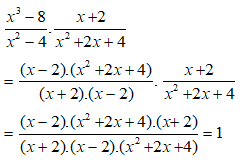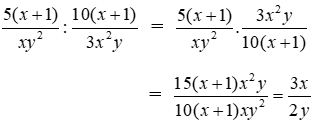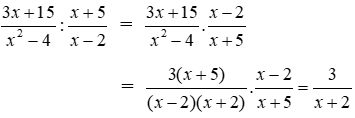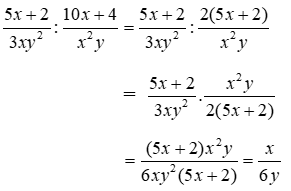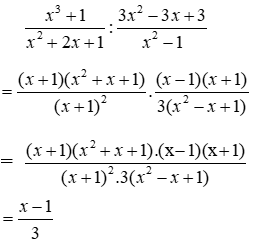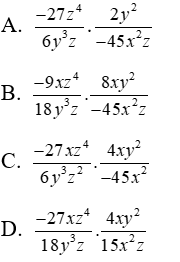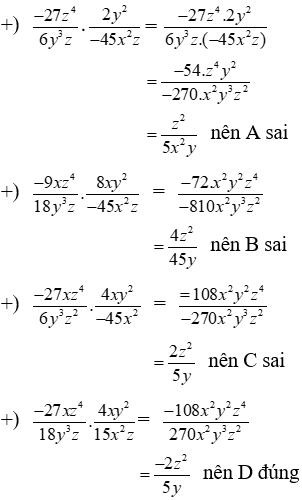60 Bài tập phép nhân các phân thức đại số (có đáp án năm 2024) - Toán 8

Phép nhân các phân thức đại số

Kiến thức cần nhớ

- Quy tắc nhân hai phân thức:

Muốn nhân hai phân thức với nhau, ta nhân các tử thức với nhau, các mẫu thức với nhau:

$\frac{A}{B}.\frac{C}{D}=\frac{A.C}{B.D}$

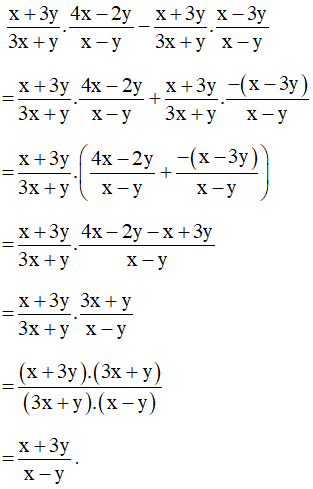
Các dạng bài tập toán phép nhân phân thức đại số

Dạng 1. Sử dụng quy tắc nhân để thực hiện phép tính.

Vận dụng quy tắc đã nêu trong phần tóm tắt lý thuyết để thực hiện yêu cầu của bài toán.

Dạng 2. Tính toán sử dụng kết hợp các quy tắc đã học.

Sử dụng hợp lý ba quy tắc đã học: quy tắc cộng, quy tắc trừ và quy tắc nhân để tính toán.

Chú ý:

+ Đối với phép nhân có nhiều hơn hai phân thức, ta vẫn nhân các tử thức với nhau và các mẫu thức với nhau.

+ Ưu tiên tính toán đối với biểu thức trong dấu ngoặc trước (nếu có).

Bài tập (có đáp án)

1. Bài tập vận dụng

Bài 1. Thực hiện các phép tính sau:

$$\begin{array}{l}a.\frac{15x}{7y^3}.\frac{2y^2}{x^2}\\ b.\frac{4y^2}{11x^4}.(-\frac{3x^2}{8y})\\ c.\frac{x^3-8}{5x+20}.\frac{x^2+4x}{x^2+2x+4}\end{array}$$

Giải:

$$\begin{array}{l}a.\frac{15x}{7y^3}.\frac{2y^2}{x^2}=\frac{15x.2y^2}{7y^3{x}^2}=\frac{30x{y}^2}{7x^2{y}^3}=\frac{30}{7xy}\\ b.\frac{4y^2}{11x^4}.(-\frac{3x^2}{8y})=-\frac{4y^2.3x^2}{11x^4.8y}=-\frac{3x^2{y}^2}{11.2x^{4}y}=-\frac{3y}{22x^2}\\ c.\frac{x^3-8}{5x+20}.\frac{x^2+4x}{x^2+2x+4}\\ =\frac{(x^3-8)(x^2+4x)}{5(x+4)(x^2+2x+4)}\\ =\frac{x(x-2)(x^2+2x+4)(x+4)}{5(x+4)(x^2+2x+4)}=\frac{x(x-2)}{5}\end{array}$$

Bài 2. Thực hiện các phép tính sau:

$$\begin{array}{l}a.\frac{5x+10}{4x-8}.\frac{4-2x}{x+2}\\ b.\frac{x^2-36}{2x+10}.\frac{3}{6-x}\end{array}$$

Giải:

$$\begin{array}{l}a.\frac{5x+10}{4x-8}.\frac{4-2x}{x+2}\\ =\frac{(5x+10).(4-2x)}{(4x-8).(x+2)}=\frac{5(x+2).2(2-x)}{4(x-2)(x+2)}\\ =\frac{5(2-x)}{2(x-2)}=-\frac{5}{2}\\ b.\frac{x^2-36}{2x+10}.\frac{3}{6-x}\\ =\frac{(x^2-36).3}{(6-x)(2x+10)}\\ =\frac{-3(6-x)(x+6)}{2(x+5)(6-x)}=-\frac{3(x+6)}{2(x+5)}\end{array}$$

Bài 3. Rút gọn biếu thức sau theo hai cách (sử dụng và không sử dụng tính chất phân phối của phép nhân đối với phép cộng:$$\frac{x-1}{x}.(x^2+x+1+\frac{x^3}{x-1})$$

Giải:

Áp dụng tính phân phối: 

$$\begin{array}{l}\frac{x-1}{x}.(x^2+x+1+\frac{x^3}{x-1})\\ =\frac{(x-1)(x^2+x+1)}{x}+\frac{(x-1)x^3}{x(x-1)}\\ =\frac{x^3-1}{x}+\frac{x^3}{x}=\frac{x^3-1+x^3}{x}=\frac{2x^3-1}{x}\end{array}$$

Không áp dụng tính phân phối:

$$\begin{array}{l}\frac{x-1}{x}.(x^2+x+1+\frac{x^3}{x-1})\\ =\frac{x-1}{x}.(\frac{(x^2+x+1)(x-1)}{x-1}+\frac{x^3}{x-1})\\ =\frac{x-1}{x}.(\frac{x^3-1}{x-1}+\frac{x^3}{x-1})=\frac{x-1}{x}.\frac{x^3-1+x^3}{x-1}\\ =\frac{(x-1)(2x^3-1)}{x(x-1)}=\frac{2x^3-1}{x}\end{array}$$

Bài 4: Đố. Đố em điền được vào chỗ trống của phép nhân dưới đây những phân  thức có mẫu thức bằng tử thức cộng với 1

$$\frac{1}{x}.\frac{x}{x+1}....=\frac{1}{x+7}$$

Giải:

$$\frac{1}{x}.\frac{x}{x+1}.\frac{x+1}{x+2}.\frac{x+2}{x+3}.\frac{x+3}{x+4}.\frac{x+5}{x+6}.\frac{x+6}{x+7}=\frac{1}{x+7}$$

Bài 5. Làm tính nhân phân thức:

$$\begin{array}{l}a.\frac{30x^3}{11y^2}.\frac{121y^5}{25x}\\ b.\frac{24y^5}{7x^2}.\left(-\frac{21x}{12y^3}\right)\\ c.\left(-\frac{18y^3}{25x^4}\right).\left(-\frac{15x^2}{9y^3}\right)\\ d.\frac{4x+8}{{\left(x-10\right)}^3}.\frac{2x-20}{{\left(x+2\right)}^2}\\ e.\frac{2x^2-20x+50}{3x+3}.\frac{x^2-1}{4{\left(x-5\right)}^3}\end{array}$$

Giải:

$$\begin{array}{l}a.\frac{30x^3}{11y^2}.\frac{121y^5}{25x}=\frac{30x^3.121y^5}{11y^2.25x}=\frac{6x^2.11y^3}{1.5}=\frac{66x^2{y}^3}{5}\\ b.\frac{24y^5}{7x^2}.\left(-\frac{21x}{12y^3}\right)=\frac{24y^5.\left(-21x\right)}{7x^2.12y^3}=\frac{2y^2.\left(-3\right)}{x}=-\frac{6y^2}{x}\\ c.\left(-\frac{18y^3}{25x^4}\right).\left(-\frac{15x^2}{9y^3}\right)=\frac{\left(-18y^3\right).\left(-15x^2\right)}{25x^4.9y^3}=\frac{-2.\left(-3\right)}{5x^2.1}=\frac{6}{5x^2}\\ d.\frac{4x+8}{{\left(x-10\right)}^3}.\frac{2x-20}{{\left(x+2\right)}^2}=\frac{4\left(x+2\right).2\left(x-10\right)}{{\left(x-10\right)}^3{\left(x+2\right)}^2}=\frac{8}{{\left(x-10\right)}^2\left(x+2\right)}\\ e.\frac{2x^2-20x+50}{3x+3}.\frac{x^2-1}{4{\left(x-5\right)}^3}=\frac{2\left(x^2-10x+25\right)\left(x+1\right)\left(x-1\right)}{3\left(x+1\right).4{\left(x-5\right)}^3}\\ =\frac{{\left(x-5\right)}^2\left(x-1\right)}{6{\left(x-5\right)}^3}=\frac{x-1}{6\left(x-5\right)}\end{array}$$

Bài 6. Rút gọn các biểu thức (chú ý dùng quy tắc đổi dấu để thay nhân tử chung):

$$\begin{array}{l}a.\frac{x+3}{x^2-4}.\frac{8-12x+6x^2-x^3}{9x+27}\\ b.\frac{6x-3}{5x^2+x}.\frac{25x^2+10x+1}{1-8x^3}\\ c.\frac{3x^2-x}{x^2-1}.\frac{1-x^4}{{\left(1-3x\right)}^3}\end{array}$$

Giải:

$$\begin{array}{l}a.\frac{x+3}{x^2-4}.\frac{8-12x+6x^2-x^3}{9x+27}=\frac{\left(x+3\right)\left(8-12x+6x^2-x^3\right)}{\left(x+2\right)\left(x-2\right).9\left(x+3\right)}\\ =\frac{2^3-{3.2}^2.x+3.2x^2-x^3}{9\left(x+2\right)\left(x-2\right)}=\frac{{\left(2-x\right)}^3}{-9\left(x+2\right)\left(2-x\right)}=-\frac{{\left(2-x\right)}^2}{9\left(x+2\right)}\\ b.\frac{6x-3}{5x^2+x}.\frac{25x^2+10x+1}{1-8x^3}=\frac{3\left(2x-1\right){\left(5x+1\right)}^2}{x\left(5x+1\right)\left[1-{\left(2x\right)}^2\right]}=\frac{3\left(2x-1\right)\left(5x+1\right)}{x\left(1-2x\right)\left(1+2x+4x^2\right)}\\ =-\frac{3\left(2x-1\right)\left(5x+1\right)}{x\left(2x-1\right)\left(1+2x+4x^2\right)}=-\frac{3\left(5x+1\right)}{x\left(1+2x+4x^2\right)}\\ c.\frac{3x^2-x}{x^2-1}.\frac{1-x^4}{{\left(1-3x\right)}^3}=\frac{x\left(3x-1\right)\left(1-x^4\right)}{\left(x^2-1\right){\left(1-3x\right)}^3}=\frac{x\left(3x-1\right)\left(x^2-1\right)\left(x^2+1\right)}{\left(x^2-1\right){\left(3x-1\right)}^3}\\ =\frac{x\left(x^2+1\right)}{{\left(3x-1\right)}^2}\end{array}$$

Bài 7: Phân tích các mẫu thức và các mẫu thức (nếu cần thì dùng phương pháp thêm và bớt cùng một hạng tử hoặc một hạng tử thành hai hạng tử) rồi rút gọn biểu thức.

$$\begin{array}{l}a.\frac{x-2}{x+1}.\frac{x^2-2x-3}{x^2-5x+6}\\ b.\frac{x+1}{x^2-2x-8}.\frac{4-x}{x^2+x}\\ c.\frac{x+2}{4x+24}.\frac{x^2-36}{x^2+x-2}\end{array}$$

Giải:

$$\begin{array}{l}a.\frac{x-2}{x+1}.\frac{x^2-2x-3}{x^2-5x+6}=\frac{\left(x-2\right)\left(x^2-2x-3\right)}{\left(x+1\right)\left(x^2-5x+6\right)}=\frac{\left(x-2\right)\left(x^2-3x+x-3\right)}{\left(x+1\right)\left(x^2-2x-3x+6\right)}\\ =\frac{\left(x-2\right)\left[x\left(x-3\right)+\left(x-3\right)\right]}{\left(x+1\right)\left[x\left(x-2\right)-3\left(x-2\right)\right]}=\frac{\left(x-2\right)\left(x-3\right)\left(x+1\right)}{\left(x+1\right)\left(x-2\right)\left(x-3\right)}=1\\ b.\frac{x+1}{x^2-2x-8}.\frac{4-x}{x^2+x}=\frac{\left(x+1\right)\left(4-x\right)}{\left(x^2-2x-8\right)x\left(x+1\right)}=\frac{4-x}{\left(x^2-4x+2x-8\right)x}\\ =\frac{4-x}{\left[x\left(x-4\right)+2\left(x-4\right)\right]x}=\frac{4-x}{x\left(x-4\right)\left(x+2\right)}=-\frac{x-4}{x\left(x-4\right)\left(x+2\right)}=-\frac{1}{x\left(x+2\right)}\\ c.\frac{x+2}{4x+24}.\frac{x^2-36}{x^2+x-2}=\frac{\left(x+2\right)\left(x+6\right)\left(x-6\right)}{4\left(x+6\right)\left(x^2+x-2\right)}=\frac{\left(x+2\right)\left(x-6\right)}{4\left(x^2+2x-x-2\right)}\\ =\frac{\left(x+2\right)\left(x-6\right)}{4\left[x\left(x+2\right)-\left(x-2\right)\right]}=\frac{\left(x+2\right)\left(x-6\right)}{4\left(x+2\right)\left(x-1\right)}=\frac{x-6}{4\left(x-1\right)}\end{array}$$

 Bài 8.   Áp dụng tính chất phân phối của phép nhân đối với phép cộng để rút gọn biểu thức:

$$\begin{array}{l}a.\frac{x^3}{x+1975}.\frac{2x+1954}{x+1}+\frac{x^3}{x+1975}.\frac{21-x}{x+1}\\ b.\frac{19x+8}{x-7}.\frac{5x-9}{x+1945}-\frac{19x+8}{x-7}.\frac{4x-2}{x+1945}\end{array}$$

Giải:

$$\begin{array}{l}a.\frac{x^3}{x+1975}.\frac{2x+1954}{x+1}+\frac{x^3}{x+1975}.\frac{21-x}{x+1}=\frac{x^3}{x+1975}.\left(\frac{2x+1954}{x+1}+\frac{21-x}{x+1}\right)\\ =\frac{x^3}{x+1975}.\frac{x+1975}{x+1}=\frac{x^3\left(x+1975\right)}{\left(x+1975\right)\left(x+1\right)}=\frac{x^3}{x+1}\\ b.\frac{19x+8}{x-7}.\frac{5x-9}{x+1945}-\frac{19x+8}{x-7}.\frac{4x-2}{x+1945}=\frac{19x+8}{x-7}.\left(\frac{5x-9}{x+1945}-\frac{4x-2}{x+1945}\right)\\ \begin{array}{cc}& =\frac{19x+8}{x-7}.\left(\frac{5x-9}{x+1945}+\frac{2-4x}{x+1945}\right)=\frac{19x+8}{x-7}.\frac{x-7}{x+1945}=\frac{\left(19x+8\right)\left(x-7\right)}{\left(x-7\right)\left(x+1945\right)}\\ & =\frac{19x+8}{x+1945}\end{array}\end{array}$$

 Bài 9. Tính tích x.y, biết rằng x và y thỏa mãn các đẳng thức sau (a, b là các hằng số):

a, (4a² – 9)x = 4a + 4; với a ≠± 3/2 và (3a³ + 3)y = 6a² + 9a với a ≠ - 1

b, (2a³ – 2b³)x – 3b = 3a; với a ≠ b và (6a + 6b)y = (a – b)² với a ≠ - b

Giải:

Bài 10. Rút gọn biểu thức:

$$\begin{array}{l}a.\frac{x^4+15x+7}{2x^3+2}.\frac{x}{14x^2+1}.\frac{4x^3+4}{x^4+15x+7}\\ b.\frac{x^7+3x^2+2}{x^3-1}.\frac{3x}{x+1}.\frac{x^2+x+1}{x^7+3x^2+2}\end{array}$$

Giải:

$$\begin{array}{l}a.\frac{x^4+15x+7}{2x^3+2}.\frac{x}{14x^2+1}.\frac{4x^3+4}{x^4+15x+7}\\ =\frac{\left(x^4+15x+7\right).x.\left(4x^3+4\right)}{\left(2x^3+2\right).\left(14x^2+1\right).\left(x^4+15x+7\right)}=\frac{4x\left(x^3+1\right)}{2\left(x^3+1\right)\left(14x^2+1\right)}=\frac{2x}{14x^2+1}\\ b.\frac{x^7+3x^2+2}{x^3-1}.\frac{3x}{x+1}.\frac{x^2+x+1}{x^7+3x^2+2}=\frac{\left(x^7+3x^2+2\right).3x.\left(x^2+x+1\right)}{\left(x^3-1\right)\left(x+1\right)\left(x^7+3x^2+2\right)}\\ =\frac{3x\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)\left(x+1\right)}=\frac{3x}{\left(x-1\right)\left(x+1\right)}\end{array}$$

2. Bài tập trắc nghiệm

Bài 1: Kết quả của phép tính 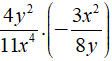 là ?

A. $\frac{- \left(3y\right)}{\left(22x^2\right) }$   

B. $\frac{\left(3y\right)}{\left(22x^2\right)}$

C. $\frac{y}{\left(11x^2\right)}$   

D. $\frac{-y}{\left(11x^2\right)}$

Lời giải:

Ta có:

Chọn đáp án A.

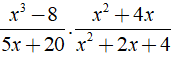
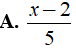
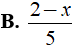
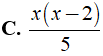
Bài 2: Rút gọn biểu thức  được kết quả là ?

Lời giải:

Ta có:

Chọn đáp án C.

Bài 3: Rút gọn biểu thức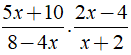 được kết quả là ?

A.$\frac{5}{2}$

B.$\frac{3}{2}$

C. $\frac{-3}{2}$  

D. $\frac{-5}{2}$

Lời giải:

Ta có:

Chọn đáp án D.

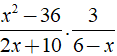
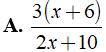
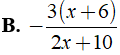
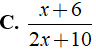
Bài 4: Rút gọn biểu thức  được kết quả là ?

Lời giải:

Ta có:

Chọn đáp án B.

Bài 5: Rút gọn biểu thức 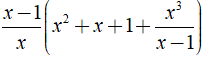 được kết quả là ?

A. $\frac{(2x^3 - 1)}{x}$   

B. $\frac{(1 - 2x^3)}{x}$

C. $\frac{1}{x}$   

D. $\frac{-1}{x}$

Lời giải:

Ta có: 

Chọn đáp án A.

Bài 6: Thực hiện phép tính

Lời giải:

Chọn đáp án A

Bài 7: Tính:

Lời giải:

Chọn đáp án A

Bài 8: Thực hiện phép tính:

Lời giải:

Chọn đáp án C

Bài 9: Tính:

A. x + y   

B. x

C. 1   

D. y

Lời giải:

Chọn đáp án C

Bài 10: Thực hiện phép tính:

Lời giải:

Chọn đáp án D

3. Bài tập tự luận

Bài 1: Kết quả của phép chia 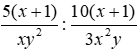 là

Lời giải

Ta có:

Bài 2: Thực hiện phép tính 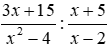 ta được?

Lời giải

Ta có:

Bài 3: Cho 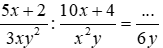. Đa thức thích hợp điền vào chỗ trống là

Lời giải

Ta có:

Vậy đa thức cần điền là x.

Bài 4: Cho 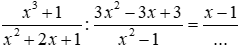. Biểu thức thích hợp điền vào chỗ trống là:

Lời giải

Ta có:

Vậy số cần điền là 3.

Bài 5: Phân thức 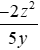 là kết quả của tích

Lời giải

Ta có:

Bài 6. Cho hai phân thức:

Cũng làm như nhân hai phân số, hãy tử với tử và mẫu với mẫu của hai phân thức này để được một phân thức.

Lời giải:

Bài 7. Làm tính nhân phân thức:

Lời giải:

Bài 8. Thực hiện phép tính:

Lời giải

Bài 9. Thực hiện phép tính:

Lời giải

Bài 10

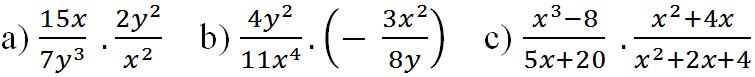
Lời giải:

a)

b)

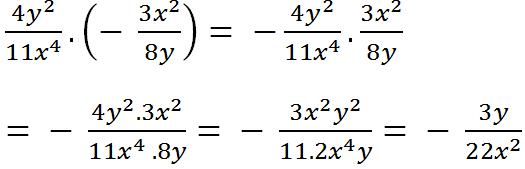
c)

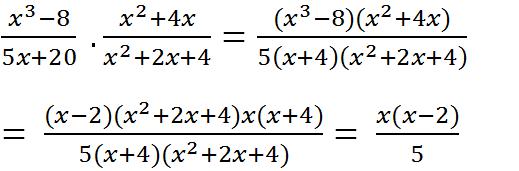
4. Bài tập làm thêm

Xem thêm các dạng Toán hay, chọn lọc khác :

60 Bài tập về Tính chất cơ bản của phân thức (có đáp án năm 2023)

60 Bài tập về Rút gọn phân thức (có đáp án năm 2023)

60 Bài tập về Quy đồng mẫu thức nhiều phân thức (có đáp án năm 2023)

60 Bài tập phép cộng các phân thức đại số (có đáp án năm 2023)

60 Bài tập về phép trừ các phân thức đại số (có đáp án năm 2023)